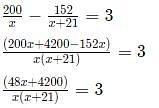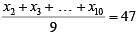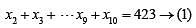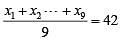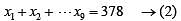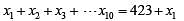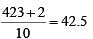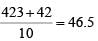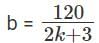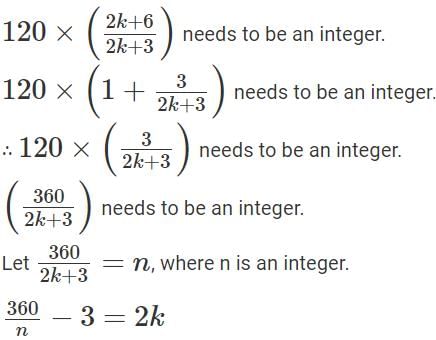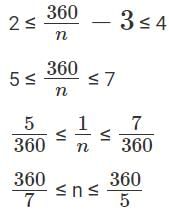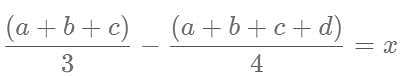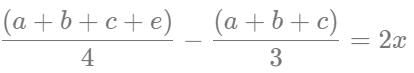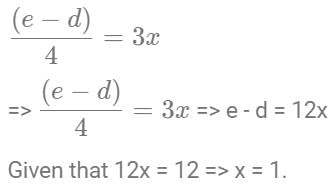CAT Previous Year Questions: Averages (June 10) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - CAT Previous Year Questions: Averages (June 10)
Ramesh and Gautam are among 22 students who write an examination. Ramesh scores 82.5. The average score of the 21 students other than Gautam is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh. The score of Gautam is
[2019]
A CAT aspirant appears for a certain number of tests. His average score increases by 1 if the first 10 tests are not considered, and decreases by 1 if the last 10 tests are not considered. If his average scores for the first 10 and the last 10 tests are 20 and 30, respectively, then the total number of tests taken by him is
[2018 TITA]
An elevator has a weight limit of 630 kg. It is carrying a group of people of whom the heaviest weighs 57 kg and the lightest weighs 53 kg. What is the maximum possible number of people in the group?
[2017 TITA]
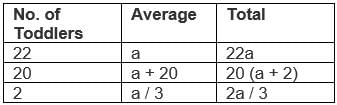
The average height of 22 toddlers increases by 2 inches when two of them leave this group. If the average height of these two toddlers is one-third the average height of the original 22, then the average height, in inches, of the remaining 20 toddlers is
[2017]
The average of 30 integers is 5. Among these 30 integers, there are exactly 20 which do not exceed 5. What is the highest possible value of the average of these 20 integers?
[2019]
In an apartment complex, the number of people aged 51 years and above is 30 and there are at most 39 people whose ages are below 51 years. The average age of all the people in the apartment complex is 38 years. What is the largest possible average age, in years, of the people whose ages are below 51 years?
[2019]
Suppose hospital A admitted 21 less Covid infected patients than hospital B, and all eventually recovered. The sum of recovery days for patients in hospitals A and B were 200 and 152, respectively. If the average recovery days for patients admitted in hospital A was 3 more than the average in hospital B then the number admitted in hospital A was
[2021]
In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by
[2020]
In an examination, the average marks of 4 girls and 6 boys is 24. Each of the girls has the same marks while each of the boys has the same marks. If the marks of any girl is at most double the marks of any boy, but not less than the marks of any boy, then the number of possible distinct integer values of the total marks of 2 girls and 6 boys is
[2023]
There are three persons A, B and C in a room. If a person D joins the room, the average weight of the persons in the room reduces by x kg. Instead of D, if person E joins the room, the average weight of the persons in the room increases by 2x kg. If the weight of E is 12 kg more than that of D, then the value of x is
[2023]
|
152 docs|327 tests
|