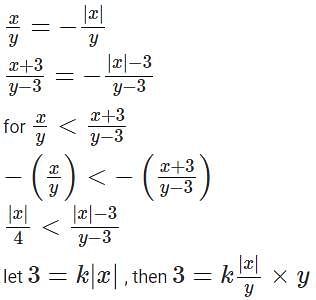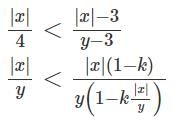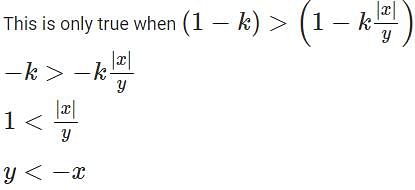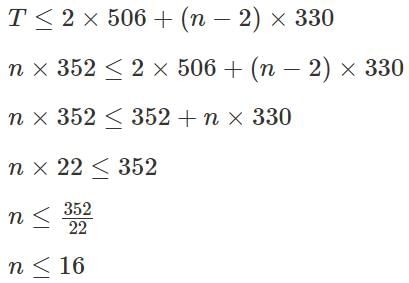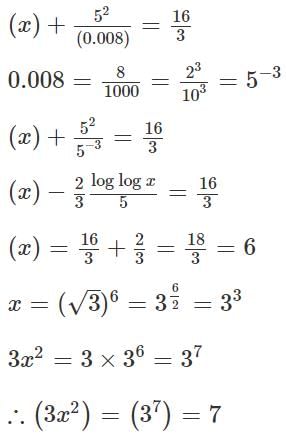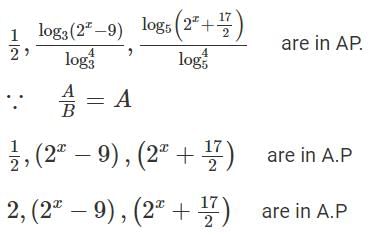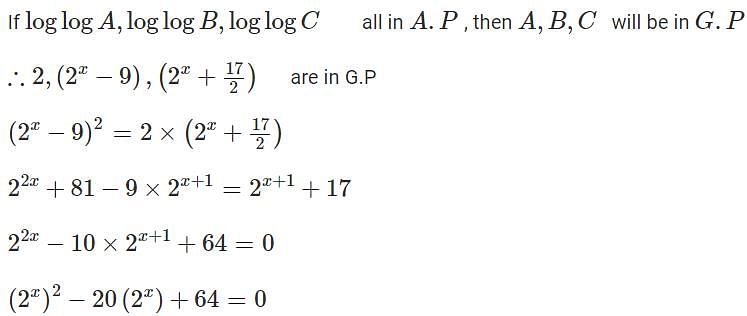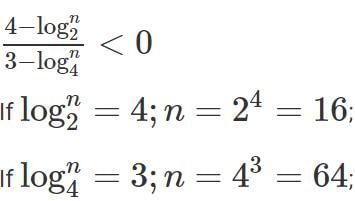CAT Previous Year Questions - Inequalities & Logarithms (July 15) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - CAT Previous Year Questions - Inequalities & Logarithms (July 15)
Any non-zero real numbers x, y such that y ≠ 3 and x/y < 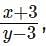 will satisfy the condition
will satisfy the condition
[2023]
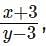 will satisfy the condition
will satisfy the conditionIf a certain amount of money is divided equally among n persons, each one receives Rs 352. However, if two persons receive Rs 506 each and the remaining amount is divided equally among the other persons, each of them receive less than or equal to Rs 330. Then, the maximum possible value of n is
[2023]
Let n and m be two positive integers such that there are exactly 41 integers greater than 8m and less than 8n (m<n), which can be expressed as powers of 2. Then, the smallest possible value of n + m is
[2023]
For natural numbers x, y, and z, if xy + yz = 19 and yz + xz = 51, then the minimum possible value of xyz is
[2022]
The number of integers n that satisfy the inequalities ∣n−60∣ < ∣n−100∣ <∣n−20∣ is
[2021]
If x and y are positive real numbers such that logx (x2 + 12) = 4 and 3 logy x = 1 , then x + y equals
[2023]
For some positive real number 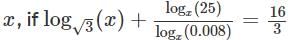 , then the value of log3 (3x2) is
, then the value of log3 (3x2) is
[2023]
For a real number x, if  are in an arithmetic progression, then the common difference is
are in an arithmetic progression, then the common difference is
[2023]
The number of distinct integer values of n satisfying 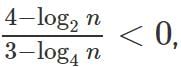 is
is
[2022]
For a real number a, if 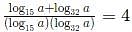 then a must lie in the range
then a must lie in the range
[2021]
|
152 docs|327 tests
|


 is always true, since We are increasing the numerator and decreasing the denominator.
is always true, since We are increasing the numerator and decreasing the denominator.
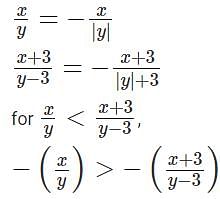
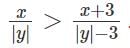 This is always true since we are increasing the numerator and decreasing the denominator.
This is always true since we are increasing the numerator and decreasing the denominator.