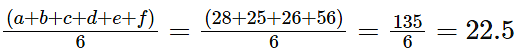CAT Previous Year Questions: Number Series- 1 (June 5) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - CAT Previous Year Questions: Number Series- 1 (June 5)
Let n be the least positive integer such that 168 is a factor of 1134n. If m is the least positive integer such that 1134n is a factor of 168m, then m + n equals [2023]
The number of all natural numbers up to 1000 with non-repeating digits is [2023]
For any natural numbers m, n, and k, such that k divides both m + 2n and 3m + 4n, k must be a common divisor of [2023]
The number of positive integers less than 50, having exactly two distinct factors other than 1 and itself, is [2023]
A school has less than 5000 students and if the students are divided equally into teams of either 9 or 10 or 12 or 25 each, exactly 4 are always left out. However, if they are divided into teams of 11 each, no one is left out. The maximum number of teams of 12 each that can be formed out of the students in the school is [2022]
Consider six distinct natural numbers such that the average of the two smallest numbers is 14, and the average of the two largest numbers is 28. Then, the maximum possible value of the average of these six numbers is [2022]
For some natural number n, assume that (15,000)! is divisible by (n!)!. The largest possible value of n is [2022]
How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7? [2020]
The mean of all 4-digit even natural numbers of the form ‘aabb’,where a > 0, is [2020]
How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3? [2020]
|
152 docs|327 tests
|