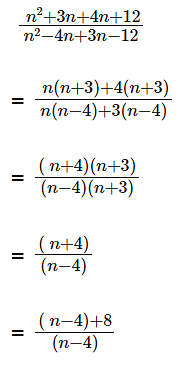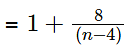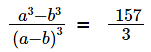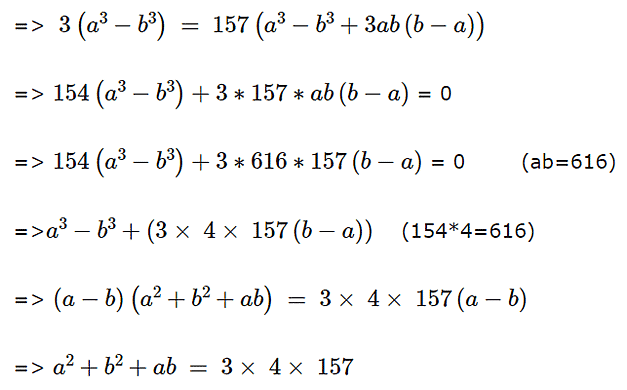CAT Previous Year Questions: Number Series- 2 (June 6) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - CAT Previous Year Questions: Number Series- 2 (June 6)
How many of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7? [2020]
Let N, x and y be positive integers such that N = x + y, 2 < x < 10 and 14 < y < 23. If N > 25, then how many distinct values are possible for N? [2020]
How many integers in the set {100, 101, 102, …, 999} have at least one digit repeated? [2020]
What is the largest positive integer n such that 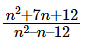 is also a positive integer? [2019]
is also a positive integer? [2019]
How many pairs (m, n) of positive integers satisfy the equation m2 + 105 = n2? [2019]
How many factors of 24 × 35 × 104 are perfect squares which are greater than 1? [2019]
In a six-digit number, the sixth, that is, the rightmost, digit is the sum of the first three digits, the fifth digit is the sum of first two digits, the third digit is equal to the first digit, the second digit is twice the first digit and the fourth digit is the sum of fifth and sixth digits. Then, the largest possible value of the fourth digit is [2019]
The product of two positive numbers is 616. If the ratio of the difference of their cubes to the cube of their difference is 157 : 3, then the sum of the two numbers is [2019]
While multiplying three real numbers, Ashok took one of the numbers as 73 instead of 37. As a result, the product went up by 720. Then the minimum possible value of the sum of squares of the other two numbers is [2018]
The number of integers x such that 0.25 ≤ 2x ≤ 200 and 2x + 2 is perfectly divisible by either 3 or 4, is [2018]
|
152 docs|327 tests
|