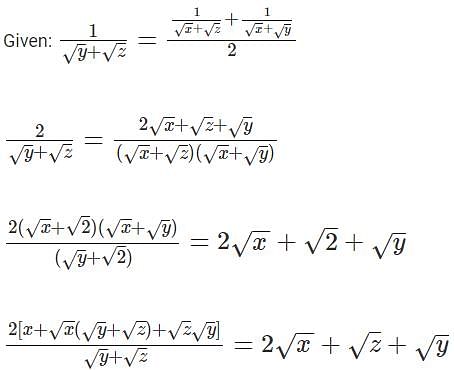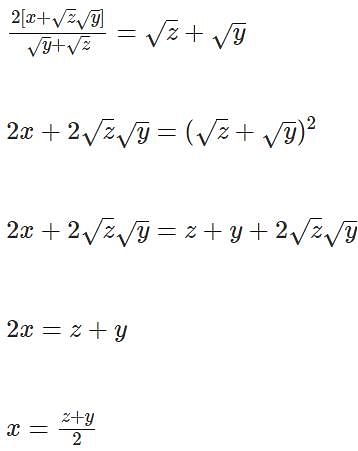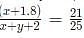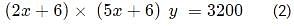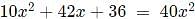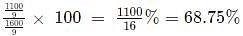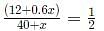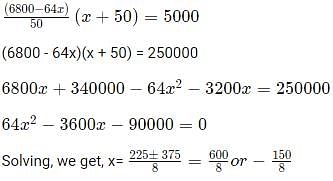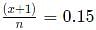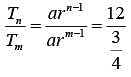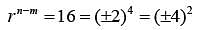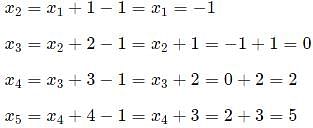CAT Previous Year Questions: Progressions (June 4) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - CAT Previous Year Questions: Progressions (June 4)
For some positive and distinct real numbers x, y and z, If 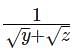 is the arithmetic mean of
is the arithmetic mean of 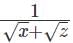 and
and  then the relationship which will always hold true, is
then the relationship which will always hold true, is
[2023]
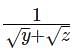 is the arithmetic mean of
is the arithmetic mean of 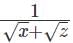 and
and  then the relationship which will always hold true, is
then the relationship which will always hold true, isIf a certain weight of an alloy of silver and copper is mixed with 3 kg of pure silver, the resulting alloy will have 90% silver by weight. If the same weight of the initial alloy is mixed with 2 kg of another alloy which has 90% silver by weight, the resulting alloy will have 84% silver by weight. Then, the weight of the initial alloy, in kg, is
[2021]
A tea shop offers tea in cups of three different sizes. The product of the prices, in INR, of three different sizes is equal to 800. The prices of the smallest size and the medium size are in the ratio 2 : 5. If the shop owner decides to increase the prices of the smallest and the medium ones by INR 6 keeping the price of the largest size unchanged, the product then changes to 3200. The sum of the original prices of three different sizes, in INR, is
[2021]
The total of male and female populations in a city increased by 25% from 1970 to 1980. During the same period, the male population increased by 40% while the female population increased by 20%. From 1980 to 1990, the female population increased by 25%. In 1990, if the female population is twice the male population, then the percentage increase in the total of male and female populations in the city from 1970 to 1990 is
[2021]
In a tournament, a team has played 40 matches so far and won 30% of them. If they win 60% of the remaining matches, their overall win percentage will be 50%. Suppose they win 90% of the remaining matches, then the total number of matches won by the team in the tournament will be
[2021]
A shop owner bought a total of 64 shirts from a wholesale market that came in two sizes, small and large. The price of a small shirt was INR 50 less than that of a large shirt. She paid a total of INR 5000 for the large shirts, and a total of INR 1800 for the small shirts. Then, the price of a large shirt and a small shirt together, in INR, is
[2021]
In a football tournament, a player has played a certain number of matches and 10 more matches are to be played. If he scores a total of one goal over the next 10 matches, his overall average will be 0.15 goals per match. On the other hand, if he scores a total of two goals over the next 10 matches, his overall average will be 0.2 goals per match. The number of matches he has played is
[2021]
A box has 450 balls, each either white or black, there being as many metallic white balls as metallic black balls. If 40% of the white balls and 50% of the black balls are metallic, then the number of non-metallic balls in the box is
[2021]
Let the m-th and n-th terms of a geometric progression be 3/4 and 12 , respectively, where m<n. If the common ratio of the progression is an integer r, then the smallest possible value of r + n - m is
[2021]
Consider a sequence of real numbers, x1 ,x2 ,x3 ,... such that xn+1 = xn + n − 1 for all n ≥ 1. If x1 =−1 then x100 is equal to
[2021]
|
152 docs|327 tests
|