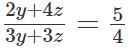CAT Previous Year Questions: Ratio & Proportion (June 17) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - CAT Previous Year Questions: Ratio & Proportion (June 17)
In a company, 20% of the employees work in the manufacturing department. If the total salary obtained by all the manufacturing employees is one-sixth of the total salary obtained by all the employees in the company, then the ratio of the average salary obtained by the manufacturing employees to the average salary obtained by the nonmanufacturing employees is
[2023]
Anil mixes cocoa with sugar in the ratio 3 : 2 to prepare mixture A, and coffee with sugar in the ratio 7 : 3 to prepare mixture B. He combines mixtures A and B in the ratio 2 : 3 to make a new mixture C. If he mixes C with an equal amount of milk to make a drink, then the percentage of sugar in this drink will be
[2023]
The number of coins collected per week by two coin-collectors A and B are in the ratio 3 : 4. If the total number of coins collected by A in 5 weeks is a multiple of 7, and the total number of coins collected by B in 3 weeks is a multiple of 24, then the minimum possible number of coins collected by A in one week is
[2023]
Pinky is standing in a queue at a ticket counter. Suppose the ratio of the number of persons standing ahead of Pinky to the number of persons standing behind her in the queue is 3 : 5. If the total number of persons in the queue is less than 300, then the maximum possible number of persons standing ahead of Pinky is
[2022]
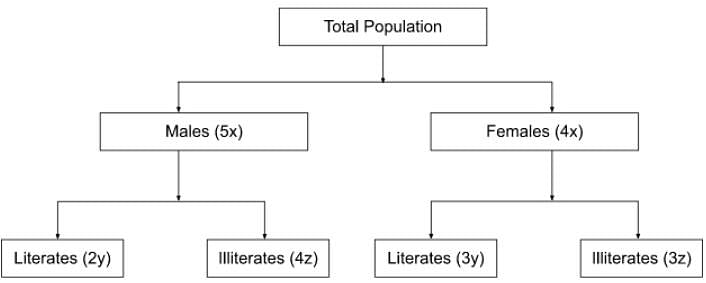
In a village, the ratio of number of males to females is 5 : 4. The ratio of number of literate males to literate females is 2 : 3. The ratio of the number of illiterate males to illiterate females is 4 : 3. If 3600 males in the village are literate, then the total number of females in the village is
[2022]
In an election, there were four candidates and 80% of the registered voters casted their votes. One of the candidates received 30% of the casted votes while the other three candidates received the remaining casted votes in the proportion 1 : 2 : 3. If the winner of the election received 2512 votes more than the candidate with the second highest votes, then the number of registered voters was
[2022]
The salaries of Ramesh, Ganesh and Rajesh were in the ratio 6:5:7 in 2010, and in the ratio 3:4:3 in 2015. If Ramesh’s salary increased by 25% during 2010-2015, then the percentage increase in Rajesh’s salary during this period is closest to
[2019]
In an examination, Rama’s score was one-twelfth of the sum of the scores of Mohan and Anjali. After a review, the score of each of them increased by 6. The revised scores of Anjali, Mohan, and Rama were in the ratio 11 : 10 : 3. Then Anjali’s score exceeded Rama’s score by
[2019]
The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is
[2019]
A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is
[2019]
|
152 docs|327 tests
|