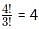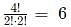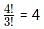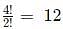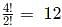CAT Previous Year Questions: Set Theory, Permutation & Combination (July 22) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - CAT Previous Year Questions: Set Theory, Permutation & Combination (July 22)
In a class of 100 students, 73 like coffee, 80 like tea and 52 like lemonade. It may be possible that some students do not like any of these three drinks. Then the difference between the maximum and minimum possible number of students who like all the three drinks is
[2022]
Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
[2020]
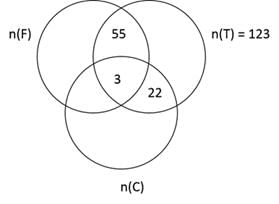
A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
[2019]
Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
[2018 TITA]
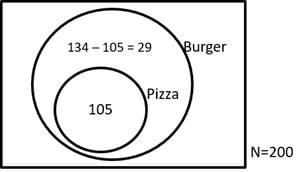
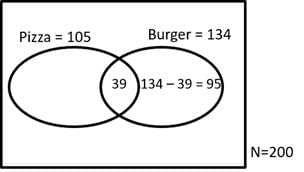
If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
[2018]
The number of groups of three or more distinct numbers that can be chosen from 1, 2, 3, 4, 5, 6, 7 and 8 so that the groups always include 3 and 5, while 7 and 8 are never included together is
[2021]
The number of ways of distributing 15 identical balloons, 6 identical pencils and 3 identical erasers among 3 children, such that each child gets at least four balloons and one pencil, is
[2021]
A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is
[2021]
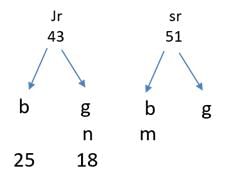
In a tournament, there are 43 junior level and 51 senior level participants. Each pair of juniors play one match. Each pair of seniors play one match. There is no junior versus senior match. The number of girl versus girl matches in junior level is 153, while the number of boy versus boy matches in senior level is 276. The number of matches a boy plays against a girl is
[2018 TITA]
The number of solutions (x, y, z) to the equation x – y – z = 25, where x, y, and z are positive integers such that x ≤ 40, y ≤ 12, and z ≤ 12 is
[2017]
|
152 docs|327 tests
|



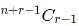 ways, where n = 3 and r = 3.
ways, where n = 3 and r = 3. 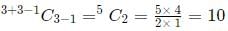
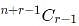 ways, where n = 3 and r = 3.
ways, where n = 3 and r = 3. 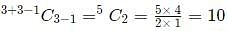
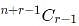 ways, where n = 3 and r = 3.
ways, where n = 3 and r = 3.