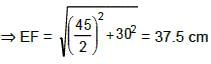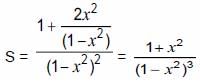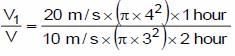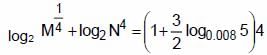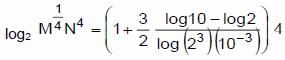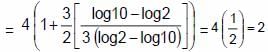CAT Quant Mock Test - 3 - CAT MCQ
25 Questions MCQ Test - CAT Quant Mock Test - 3
DIRECTIONS for questions: Select the correct alternative from the given choices.
The function g(x) = |x – 4| + |4.5 – x| + |4.8 – x|, where x is a real number, attains its minimum value at
(a)x = 4.1
(b)x = 4.4
(d)None of the above
DIRECTIONS for questions: Select the correct alternative from the given choices.
Each of the numbers a1, a2, a3, - - - an, where n ≥ 3m is equal to 1 or –1. Suppose a1 a2 a3 + a2 a3 a4 + a3 a4 a5 + - - - + an – 3 an – 2 an – 1 + an – 2 an – 1 an + an – 1 an a1 + an a1 a2 = 0, then
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
DIRECTIONS for questions: Select the correct alternative from the given choices.
There are five pipes P1, P2, P3, P4 and P5 which can fill a tank in 45, 30, 15, 10 and 9 minutes respectively. Exactly two of the pipes are now converted into emptying pipes retaining the same respective flow rates. If one filling pipe and one emptying pipe operate, the empty tank gets filled in 12 6 / 7 minutes, while for another combination of a filling pipe and an emptying pipe, the full tank gets emptied in 22 x 1 / 2 minutes. Which of the following pipes may have been converted into emptying pipes?
DIRECTIONS for questions: Select the correct alternative from the given choices.
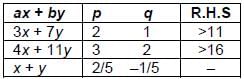
If 2x + 3y > 6 and y – x > – 1, the sign of which of the following expressions can be uniquely determined?
I. 3x + 7y
II. 4x + 11y
III. x + y
DIRECTIONS for questions: Select the correct alternative from the given choices.
A graph is defined as a set of points connected by lines called edges. Each edge connects a pair of points. It is possible to reach any point from any other point through a sequence of edges. Consider a graph with 15 points. If the number of edges in the graph is denoted by e, then which of the following best describese?
DIRECTIONS for questions: Select the correct alternative from the given choices.
If the equation (x – k)2 + (y + k)2 = 9, represents a circle, with centre O, in the co-ordinate plane and k is a positive constant, then which of the following is an appropriate representation of the graph in the co-ordinate plane?
DIRECTIONS for question: Select the correct alternative from the given choices.
The median of a set of eight numbers is ‘m ’. If a number larger than the largest number in the set is included, the median increases by 4. If the largest number in the set is removed, the median becomes m / 2. Find the median, if a number smaller than the least number in the set is included.
DIRECTIONS for questions: Answer the questions on the basis of the information given below.
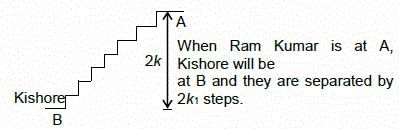
Ram Kumar wanted to come down from the first floor to the ground floor of a shopping mall, whereas Kishore wanted to climb up from the ground floor to the first floor. Both used the same escalator (a moving staircase) which was ascending from the ground floor to the first floor and both walked towards their respective destinations at their normal speeds. Both of them started simultaneously from the top and the bottom of the escalator respectively and crossed each other after exactly 21 seconds. If instead, Kishore had walked at 1/3rd of his normal speed while Ram Kumar maintained his normal speed, they would have crossed each other after exactly 28 seconds from the start. Further, if both Ram Kumar and Kishore had climbed up from the ground floor to the first floor using the same ascending escalator, walking at their normal speeds, the number of steps taken by Kishore to reach the first floor would be 20% less than the number of steps taken by Ram Kumar for the same.
Q.Ram Kumar walked down from the first floor to the ground floor using the same escalator. However, after some time the escalator stopped moving due to a power failure. Find the total time taken by Ram Kumar to reach the ground floor, given that the time for which he walked on the moving escalator was the same as that for which he walked on the stationary escalator.
DIRECTIONS for questions: Select the correct alternative from the given choices.
If set A contains five elements and set B contains four elements, how many different onto mappings from A to B are possible?
DIRECTIONS for questions: Select the correct alternative from the given choices.
Spending Rs.422, Ranjit bought 35 pens from among three varieties of pens – A, B, C. If each pen of varieties A, B, and C costs Rs.10, Rs.8, and Rs.15 respectively, and Ranjit bought the maximum possible pens of variety C, find the total number of pens of varieties A and B that he bought.
DIRECTIONS for questions: Select the correct alternative from the given choices.
In a class of n students, the students who get more than 70% are awarded Distinction. Among these students, those who get more than 90% are also awarded a Certificate of Merit. In how many possible ways could Distinction and Certificates of Merit be secured by the students in the class?
DIRECTIONS for questions: Select the correct alternative from the given choices.
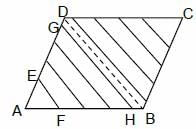
A parallelogram is divided into nine regions of equal area by drawing line segments parallel to one of its diagonals. What is the ratio of the length of the longest of the line segments to that of the shortest?
DIRECTIONS for questions: Select the correct alternative from the given choices.
A had a certain amount of money. B had seven times the amount that A had. A bought a certain number of gold coins and was left with one-third the cost of a gold coin. B bought as many gold coins as he could and found that, if he had Rs.7,500 more, he could have bought one more gold coin. Find the cost of each gold coin.
DIRECTIONS for questions: Select the correct alternative from the given choices.
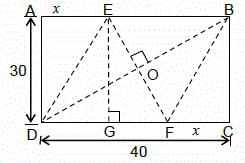
A rectangular piece of paper is folded in such a way that one pair of diagonally opposite vertices coincide. If the dimensions of the rectangle are 40 cm × 30 cm, what is the length (in cm) of the fold?
DIRECTIONS for questions: Select the correct alternative from the given choices.
M workers started a job. At the end of theith day of the job, where 1 ≤ i ≤ M, the ith worker left the job. The job was completed when the Mth worker left. If the ith worker can do i units of work per day and the job to be done was equal to 204 units of work, find M.
DIRECTIONS for questions: Select the correct alternative from the given choices.
If x and y are positive integers and x2 + y2 = 1800, then the maximum value ofx + y is
DIRECTIONS for questions: Select the correct alternative from the given choices.
There are 2272 students in a school. All the students stand in a row, from left to right, holding a number such that the number with any student (except those at the ends) equals the sum of the numbers with the student on his immediate left and the student on his immediate right. If the numbers with the 1136thand 1137thstudents from the left end are – 57 and 16 respectively, then find the sum of the numbers with all the students.
DIRECTIONS for questions: Select the correct alternative from the given choices.
If the areas of the six faces of a cuboid are a1, a2, ……. a6, then the volume of the cuboid is
DIRECTIONS for questions: Select the correct alternative from the given choices.
If both p and q belong to the set {1, 2, 3, 4}, find the number of equations of the form 2x− px + q = 0, which have real roots.
DIRECTIONS for questions: Select the correct alternative from the given choices.
In a certain class, there are two sections – A and B – with equal number of students in each section. The average height ofthe students of section A is 155 cms and that of section B is 160 cms. One-fourth of the students from section B move to section A, thereby increasing the average height of section A by 1 cm. What happens to the average height of section B after this movement of students to section A?
DIRECTIONS for questions : Select the correct alternative from the given choices. Given that |x| < 1, find the value of 1 + 4x2+ 9x4 + 16x6 + 25x8 ….∞.
(d)1 + x2 / (1 – x2)3
DIRECTIONS for questions: Select the correct alternative from the given choices.
The sum (S) of the squares of the first n natural numbers is equal to the sum of the first 2n natural numbers. What is the remainder when S is divided by 2n?
DIRECTIONS for questions: Select the correct alternative from the given choices.
Water flowing at a speed of 10 m/s, through a cylindrical pipe of length 20 m and diameter 6 cm, can fill a tank of volume V in 2 hours. The volume of the tank that can be completely filled by water flowing at a speed of 20 m/s, through a cylindrical pipe of length 40 m and of radius 4 cm, in 1 hour is
DIRECTIONS for questions: Select the correct alternative from the given choices.
If ![]() , which of the following is true?
, which of the following is true?
DIRECTIONS for questions: Select the correct alternative from the given choices.
The age of a person k years ago was half of what his age would bek years from now. The age of the same personp years from now would be thrice of what his age was p years ago. What is the value of the ratiok : p?