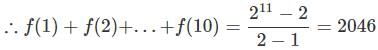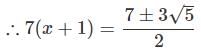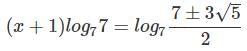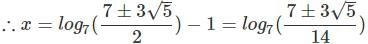CAT Quantitative Aptitude MCQ - 2 - CAT MCQ
30 Questions MCQ Test - CAT Quantitative Aptitude MCQ - 2
5 men and 6 women are to be arranged in a straight line for a photograph. In how many ways this can be done such that two particular women Sheela and Chameli are always together and no two men are beside each other?
What will be the number of zeroes at the end of the product of the first 40 natural numbers?
The speed of the boat in still water is 6 km/h and the speed of the river is 1.2 km/h. Boat takes a total of 10 h to go to a place and come back. What is the total distance covered in the whole process?
The total number of relations from set P to set Q are 4096. If x and y are the number of elements in sets P and Q respectively, find the number of values the ordered pair (x, y) can take.
The annual income of X and Y is in the ratio 6 : 5 and their expenses are in the ratio 9 : 7. If each saves Rs. 3000 at the end of the year, find the sum of their annual incomes.
The sum of three numbers is zero and the the product of the three numbers is -120, find the sum of the cubes of the three numbers.
The per month average salary of the employees of a firm is Rs. 20,000. All the employees are given a raise of 15% after the appraisal month. However, some people resigned from the firm and the funds allocated towards giving away their salary was distributed amongst all. Resultantly, the average rise in the salary of the currently working employees increased by Rs. 2,000. If 46 employees are currently working with the company then find the number of employees who resigned.
The 3rd term of an A.R is 23 and 8th term is 58. Find the 80th term.
On planet K-Pax, the dial of a clock has 14 equally spaced markings. The day is divided into 28 hours; each hour is divided into 70 minutes and each minute is divided into 70 seconds. Find that number of times that the hour hand and minute are exactly opposite to each other in a day.
What is the value of x + √x, if log2 X + log2 X2 + log2 X3 +...+ log2 X10= 440?
A train 125 m long passes a man, running at 5 km/hr in the same direction in which the train is going, in 10 seconds. The speed of the train is:
The ratio of the sum to product of two digits of a two-digit number is 2 : 3. If one of the digits exceeds the other by 4, then find the number of highest value which can be formed using the two digits.
What will be the co-ordinates of the foot of the perpendicular drawn from the point (3, 4) to the line 4x + 2y - 9 = 0?
The roots of the quadratic equation x2 + bx + c = 0, having distinct roots, are non-zero and integral solutions of the inequality, y2 + 2y - 3 < 0. What is the value of b + c?
A family spends Rs. 3,000 per month to purchase 15 kg grocery. If the rate per kg of the grocery increases by 20%, how much less grocery (in kg) should the family purchase to keep the expenditure same?
What is the diagonal of a square (in cm) having its area equal to that of a rhombus having its diagonals as 12 cm and 14 cm?
A train 440 metres long passes a railway platform 876 metres long in 10 seconds. How many seconds will it take to pass a running train 990 metres long? (Enter 0 if the answer cannot be determined.)
Find the selling price of a sari after successive discounts of 20%, 25% and 30% on the marked price of Rs. 700.
Two circles with different radii touch each other in one point such that the smaller circle lies completely inside the larger circle. The smaller circle has point O as the center. A chord AB of the larger circle is tangent to the smaller circle. AB touches smaller circle at point C. A and B lies on the circumference of the larger circle. If BC = 10 cm and OB = 20 cm. Find OC (in cm).
The average salary per employee in an office is Rs. 3,200 per month. The average salary of officers is Rs. 6,800 and that of non-officers is Rs. 2,000. If the number of officers is 5, then find the number of non-officers in the office.
In a set of 17 points, exactly 5 points are collinear. How many triangles can be formed using these points? (Assume all points are distinct)
The perimeter of an isosceles triangle is equal to 14 cm and the ratio of the lateral side and the base is 5 : 4. Find the area of the triangle (in cm2)
If 'f' is the real function satisfying 2f(xy) = [f(x)]y + [f(y)]x for all real values of x, y and f(1) = 2, then f(1) +f(2)+f(3) + ... +f(10) is equal to
If 343x+2 - 49x+3 + 7x+4 = 0, which of these could be a value for x?
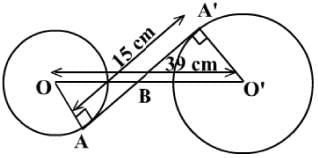
The length of the common tangent of two circles of different radius is 15 cm and it divides the line joining the centre of the two circles in the ratio 2 : 1. Find the area of the larger circle if the length of the line joining the centre of two circles is 39 cm.
Sushil is standing 25 m away from a tower. If the angle of elevation of the tower from this point is 45°, find the height (in m) of the tower.
X alone takes 5 days and Y alone takes 7 days to finish a job. How many days will X and Y take to finish the job working on alternate days starting with X?



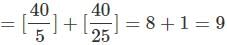
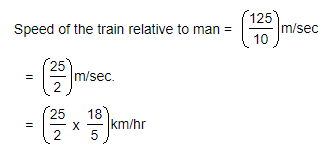
 x - 5 = 45
x - 5 = 45  x = 50 km/hr.
x = 50 km/hr.