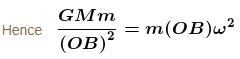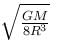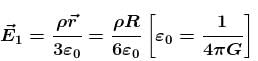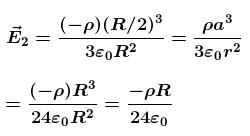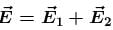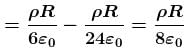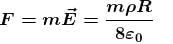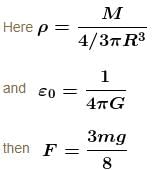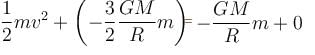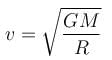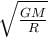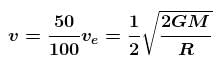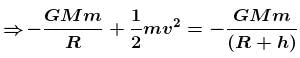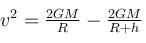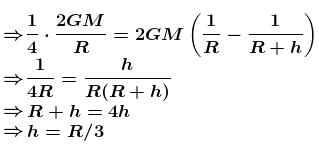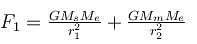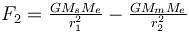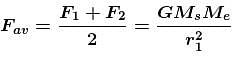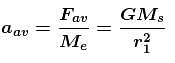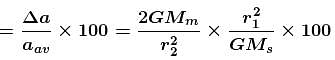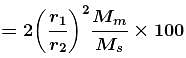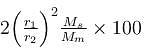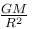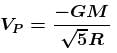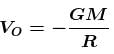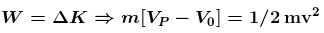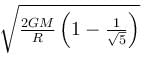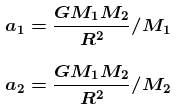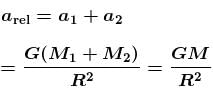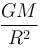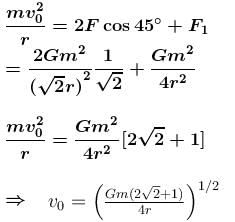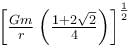Central Forces MCQ Level – 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Central Forces MCQ Level – 2
The gravitational potential of two homogeneous spherical shells A and B of same surface density at their respective centres are in the ratio 3 : 4. If the two shells coalesce into single one such that surface density remains same, then the ratio of potential at an internal point of the new shell of shell A is equal to :
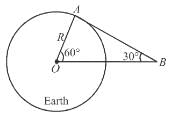
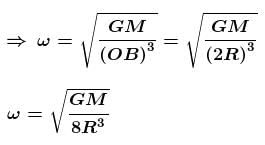
A satellite is launched in the equatorial plane in such a way that it can transmit signals upto 60° latitude on the earth. The angular velocity of the satellite is :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
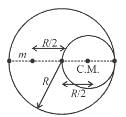
A cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity).
[Here, g = GM/R2, where M is the mass of the sphere without cavity ]
A tunnel is dug along the diameter of the earth (Radius R and mass M ). There is a particle of mass m at the centre of the tunnel. The minimum velocity given to the particle so that it just reaches to the surface of the earth is :
Maximum height reached by a rocket fired with a speed equal to 50% of the escape velocity from earth’s surface is :
The percentage change in the acceleration of the earth towards the sun from a total eclipse of the sun to the point where the moon is on a side of earth directly opposite to the sun is :
A small area is removed from a uniform spherical shell of mass M and radius R. Then the gravitational field intensity near the hollow portion is :
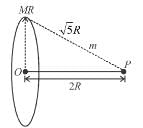
A point P lies on the axis of a fixed ring of mass M and radius R, at a distance 2R from its centre O. A small particle starts from P and reaches O under gravitational attraction only. Its speed O will be
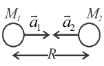
Two particles of combined mass M, placed in space with certain separation, are released. Interaction between the particles is only of gravitational nature and there is no external force present. Acceleration of one particle with respect to the other when separation between them is R, has a magnitude :
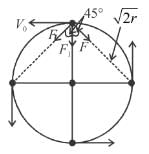
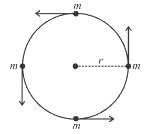
Four similar particles of mass m are orbiting in a circle of radius r in the same angular direction because of their mutual gravitational attractive force. Velocity of a particle is given by :


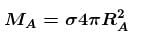
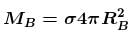 where σ is surface density
where σ is surface density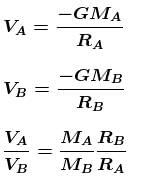
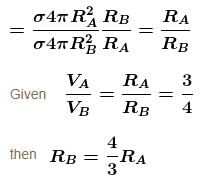
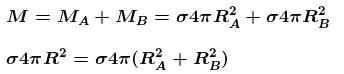

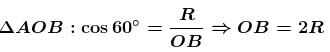 (where OR is orbital radius)
(where OR is orbital radius)