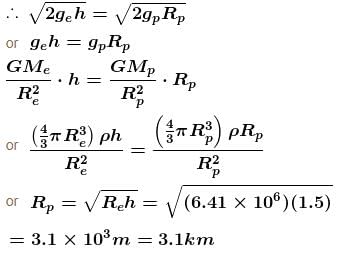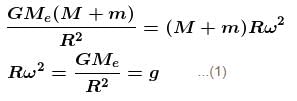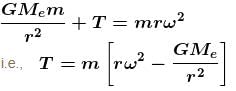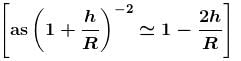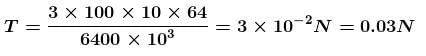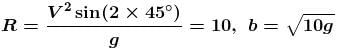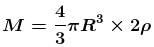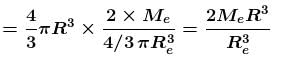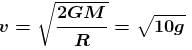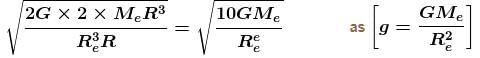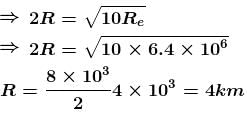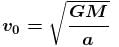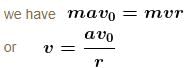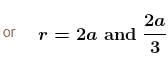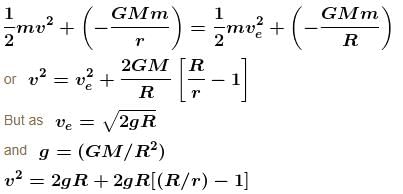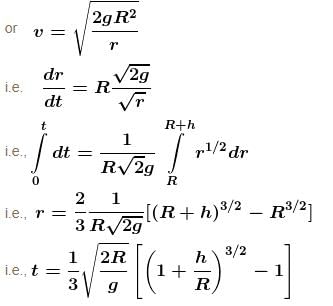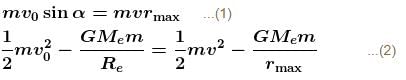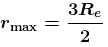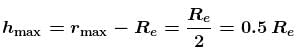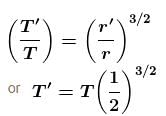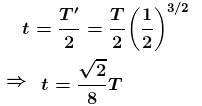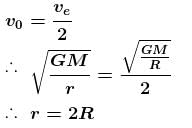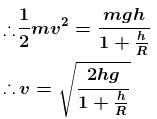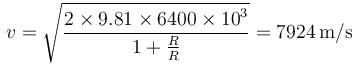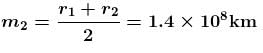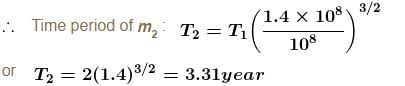Central Forces NAT Level – 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Central Forces NAT Level – 2
A man can jump vertically to a height of 1.5m on the earth. Calculate the radius of a planet (in kms ) of the same mean density as that of the earth from whose gravitational field he could escape by jumping. Radius of earth is 6.41 × 106m.
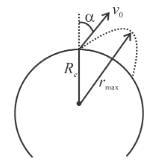
A particle is projected from point A that is at a distance 4R from the centre of the Earth will speed v1 in a direction making joining the centre of the Earth and point A as shown.find the speed v2 if particle passes grazing the surface of the earth Constant interaction only between these two Express you answer in the form (500 × √2X)m/s and write the value of X?

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A cord of length 64m is used to connect a 100kg astronaut. Estimate the value of the tension (in Newton) in the cord. Assume that the spaceship is orbiting near earth surface. Also assume that the spaceship and the astronaut fall on a straight line from the earth’s centre. The radius of the earth is 6400km.
Ravi can throw a ball a speed on earth which can cross a river of width 10m. Ravi reaches on an imaginary planet whose mean density is twice of the earth. If maximum radius of planet so that if Ravi throws the ball at same speed it may escape from planet is xkm. then x is.
(Given radius of earth = 6.4 × 106m.)
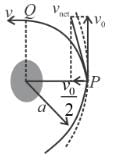
An earth satellite is revolving in a circular orbit of radius a with velocity v0. There is a gun in the satellite and is aimed directly towards the earth. A bullet is fired from the gun with muzzle velocity 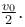 Neglecting resistance offered by cosmic dust and recoil of gun, the maximum and minimum distance of bullet from the centre of earth during its subsequent motion is na and
Neglecting resistance offered by cosmic dust and recoil of gun, the maximum and minimum distance of bullet from the centre of earth during its subsequent motion is na and 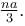 Find the value of n.
Find the value of n.
A body is projected vertically upwards from the surface of earth with a velocity sufficient to carry it to infinity. The time taken by it to reach height h is given by 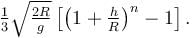 Find the value of n.
Find the value of n.
A projectile of mass m is fired from the surface of the earth at an angle α = 60° from the vertical. The initial speed v0 is equal to 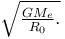 The height projectile rises is given by nRe. Find the value of n. Neglect air resistance and the earth’s rotation.
The height projectile rises is given by nRe. Find the value of n. Neglect air resistance and the earth’s rotation.
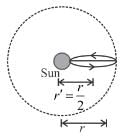
If a planet was suddenly stopped in its orbit supposed to be circular, it will fall onto the sun in a time 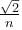 times the period of the planet’s revolution. Find the value of n.
times the period of the planet’s revolution. Find the value of n.
An artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the surface of earth. (Radius of the earth = 6400km ). If the satellite is stopped suddenly in its orbit and allowed to fall freely on the earth, find the speed (in m/s) with which it hits the surface of earth.
Two planets of equal mass orbit a much more massive star (figure). Planet m1 moves in a circular orbit of radius 1 × 108km with period 2year. Planet m2 moves in an elliptical orbit with closed distance r1 = 1 × 108km and farthest distance r2 = 1.8 × 108km, as shown.
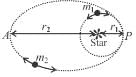
Using the fact that the mean radius of an elliptical orbit is the length of the semi-major axis, find the period of m2's orbit.