Circles - Olympiad Level MCQ, Class 9 Mathematics - Class 9 MCQ
25 Questions MCQ Test - Circles - Olympiad Level MCQ, Class 9 Mathematics
AB is a chord of length 24 cm of a circle with centre O and radius 13 cm. Find the distance of the chord from the centre.
48 cm long chord of a circle is at a distance of 7 cm from the centre. Find the radius of the circle.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A chord of a circle is 12 cm in length and its distance from the centre is 8 cm. Find the length of the chord of the same circle which is at a distance of 6 cm from the centre.
Which of the following statement(s) is / are true ?
In the given figure, find the value of x.
In the given figure, ΔABC is inscribed in a circle with centre O. If ∠ACB = 65°, find ∠ABC.
In the given figure if O is the center of the circle, then find x.
An equilateral triangle PQR is inscribed in a circle with centre O. Find ∠QOR.
In the given figure, ΔXYZ is inscribed in a circle with centre O. If the length of chord YZ is equal to the radius of the circle OY then ∠YXZ =
In the given figure, O is the centre of a circle. If ∠DAC = 54° and ∠ACB = 63° then ∠BAC =
In the given figure, AOB is a diameter of a circle with centre O. If ∠BOD = 120°, find ∠ACD.
AB is a chord of a circle with centre O and radius 17 cm. If and OM = 8 cm, find the length of chord AB.
In the given figure, O is the centre of the circle. Find the value of x.
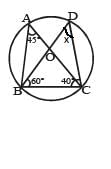
In the given figure, ABCD is a quadrilateral incribed in a circle. Diagonals AC and BD are joined. If ∠CAD = 50° and ∠BDC = 45°. Find ∠BCD.
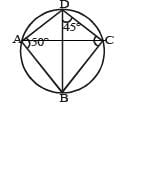
Find the value of x ( ∠BCD) in the given figure.
In the given figure, two chords AB and CD of a circle intersect each other at a point E such that ∠BAC = 45°, ∠BED = 120°. Then find ∠ABD.
In the given figure, AOB and COD are two diameters of a circle with centre O. If ∠OAC = 60°. Find ∠ABD.
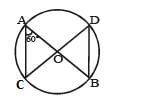
In the given figure, ABCD is a quadrilateral inscribed in a circle. Diagonals AC and BD are joined. If ∠CAD = 40° and ÐBDC = 25°. Find ∠BCD.
Two chords AB and CD of a circle cut each other when produced outside the circle at P. AD and BC are joined. If ∠PAD = 30° and ∠CPA = 45°. Find ∠CBP
In the given figure, DABC is inscribed in a circle. The bisector of ∠BAC meets BC at D and the circle at E. If EC is joined then ∠ECD = 30°. Find ∠BAC.
In the given figure, ABCD is a cycle quadrilateral in which ∠BAD = 120°. Find ∠BCD.
In the given figure POQ is a diameter of a circle with centre O and PQRS is a cyclic quadrilateral. SQ is joined. If ∠R = 138°, find ∠PQS.
In the given figure, PQRS is a cyclic trapezium in which PQ || SR. If ∠P = 82°. Find ∠S.
Two circles intersect in A and B. Quadrilaterals PCBA and ABDE are inscribed in these circles such that PAE and CBD are line segment. If ∠P = 95° and ∠C = 40°. Find the value of Z.
Which of the following statement(s) is / are true ?

















