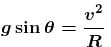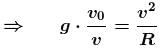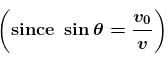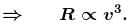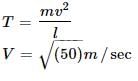Circular Motion MCQ Level - 1 - Physics MCQ
10 Questions MCQ Test - Circular Motion MCQ Level - 1
A stone tied to a string is rotated in a vertical plane. If mass of the stone is m, the length of the string is R and the linear speed of the stone is v when the stone is at its lowest point, then the tension in the string at the lowest point will be :
A ring of radius R lies in vertical plane. A bead of mass m can move along the ring without friction. Initially the bead is at rest at the bottom most point on ring. The minimum constant horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle :

When the road is dry and coefficient of friction is μ the maximum speed of a car in a circular path is 10ms–1. If the road becomes wet and coefficient of friction become μ/4, what is the maximum speed permitted?
A car of mass M is traveling on a horizontal circular path of radius r. At an instant its speed is v and tangential acceleration is a :
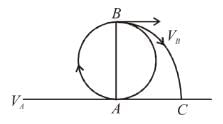
A body is tied up by a string of length l and rotated in vertical circle at minimum speed. When it reaches at highest point string breaks and body moves on a parabolic path in presence of gravity according to figure. In the plane of point A, value of horizontal range AC will be :
The maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
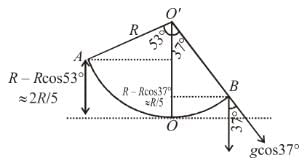
A section of fixed smooth circular track of radius R in vertical plane is shown in the figure. A block is released from position A and leaves the track at B. The radius of curvature of its trajectory when it just leaves the track at B is:
A particle of mass m begins to slide down on a fixed smooth sphere from the top. What is its tangential acceleration when it breaks off the sphere?
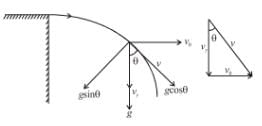
A particle is projected horizontally from the top of a tower with a velocity v0. If v be its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :
The breaking tension of a string is 10N. A particle of mass 0.1kg tied to it is rotated along a horizontal circle of radius 0.5metre. The maximum speed with which the particle can be rotated without breaking the string is :


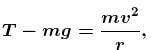 (centripetal force at lowest point)
(centripetal force at lowest point)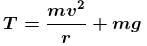
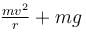

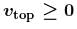
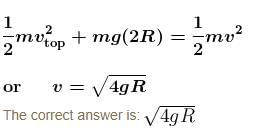

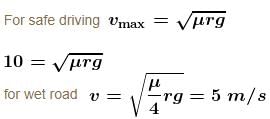
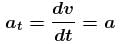
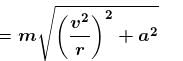
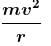
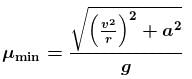
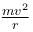
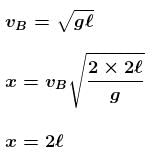
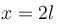
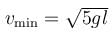
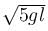
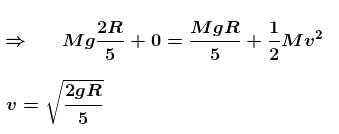
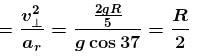
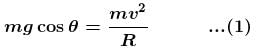
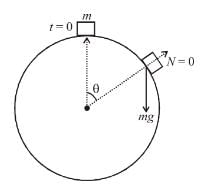
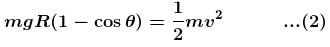
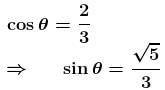
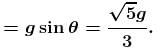
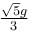
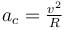 (centripetal acceleration)
(centripetal acceleration)