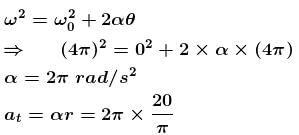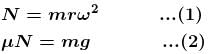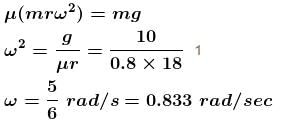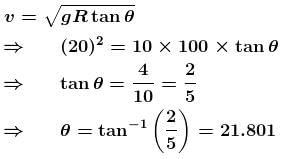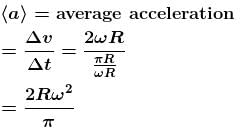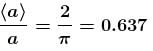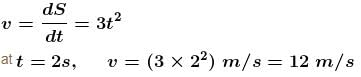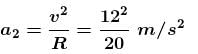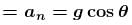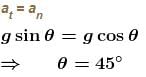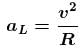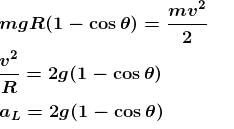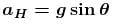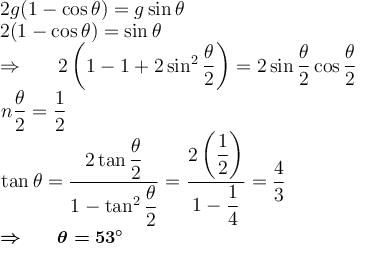Circular Motion NAT Level - 1
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics | Circular Motion NAT Level - 1
| 1 Crore+ students have signed up on EduRev. Have you? |
A particle moves along a circle of radius (20/π)m with tangential acceleration of constant magnitude. If the speed of the particle is 80 m/s at the end of the second revolution after motion has begun. What will be the tangential acceleration in ms–2?
n = 2 revolution
v = 80 m/s
from 3rd equation of motion
= 40 m/s2
The correct answer is: 40
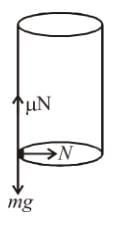
In the motorcycle stunt called ‘the well of death’ the track is a vertical cylindrical surface of 18 m radius. Take the motorcycle to be a point mass and µ = 0.8. The minimum angular speed (rad/sec) of the motorcycle to prevent him from sliding down should be :
From (1) and (2)
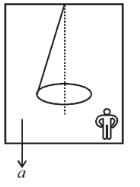
In the figure shown a lift goes downwards with a constant retardation. An observer in the lift observes a conical pendulum in the lift, revolving in a horizontal circle with time period 2 seconds. The distance between the centre of the circle and the point of suspension is 2.0 m. The retardation of the lift in m/s2 is :
geff = g + a
Put T = 2
⇒ a = 10 m/s2
The correct answer is: 10
A circular curve of a highway is designed for traffic moving at 72 km/h. If the radius of the curved path is 100 m, the correct angle (in degree) of banking of the road should be given by :
The correct answer is: 21.801
For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?
Instantaneous acceleration = ω2R
The correct answer is: 0.637
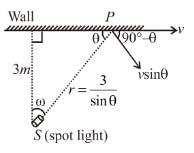
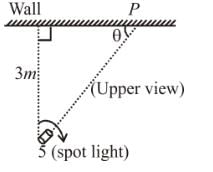
A spot light S rotates in a horizontal plane with a constant angular velocity of 0.1 rad/s. The spot of light P moves along the wall at a distance 3m. What is the velocity in ms–1 of the spot P when θ = 45°?
The correct answer is: 0.6
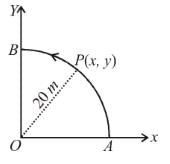
A point P moves in counter clockwise direction on a circular path as shown in the figure. The movement of 'P' is such that it sweeps out a length s = t3 + 5, where s is in metres and t is in seconds. The radius of the path is 20 m. The acceleration in ms–2 of 'P' when t = 2s is nearly.
S = t3 + 5
Linear speed of the particle
Linear acceleration 
at t = 2s, a1 = 12 m/s2
The centripetal acceleration 
The correct answer is: 14
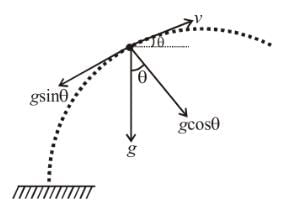
A stone is projected from level ground at t = 0 sec such that its horizontal and vertical components of initial velocity are 10 m/s and 20 m/s respectively. Then the instant of time (in seconds) at which tangential and normal components are acceleration of stone are same is : (neglected air resistance) g = 10m/s2
Tangential acceleration
Normal acceleration 
During upward motion
⇒ vy = vz
uy – gt = ux
20 – 10t = 10
⇒ t = 1 sec
During downward motion
at = an
vy – vx
20 – 10t = – 10
⇒ t = 3 sec
The correct answer is: 3
A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (in degree) in the extreme position is?
Acceleration at lowest position
From energy conservation
acceleration at highest position
according to problem aL = aH
The correct answer is: 53
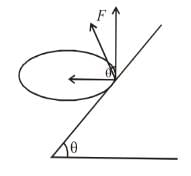
A bird is flying in air. To take a turn in the horizontal plane of radius R = 10m with the velocity v = 10m/s at what angle (in degree) it should bend with the horizontal.
The correct answer is: 45
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Download free EduRev App
Related content with Circular Motion NAT Level - 1
|
|
|
|
Related tests with Circular Motion NAT Level - 1
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
