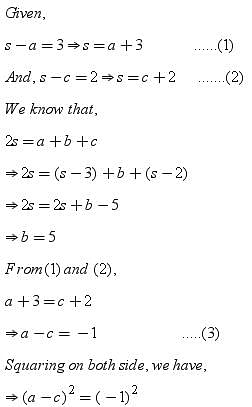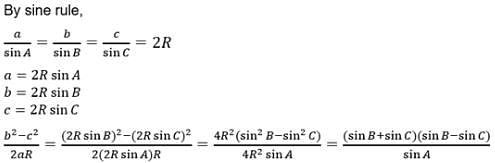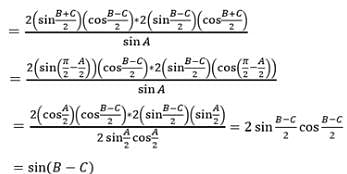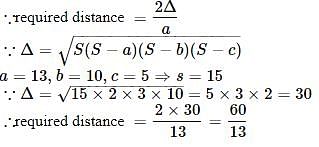Competition Level Test: Solution Of Triangles- 1 - Class 11 MCQ
30 Questions MCQ Test - Competition Level Test: Solution Of Triangles- 1
In a ΔABC, A : B : C = 3 : 5 : 4. Then a + b + c√2 is equal to
If in a ΔABC,  =
= 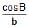 =
= 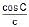 , then the triangle is
, then the triangle is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a triangle ABC, (a + b + c) (b + c – a) = kbc, if
If in a triangle ABC, right angle at B, s – a = 3 and s – c = 2, then
In a ΔABC if b + c = 3a, then cot B/2 . cot C/2 has the value equal to
In a ΔABC, A = 2π/3, b - c = 3√3 cm and ar(ΔABC) = 9√3/2 cm2. Then a is
If in a ΔABC, Δ = a2 – (b – c)2, then tan A =
If R denotes circumradius, then in ΔABC, is equal to
If a ΔABC, if b = 2 cm, c = √3 and ∠A = π/6, then values of R is equal to
In a ΔABC, the value of is equal to
If the sides of a triangle are 3 : 7 : 8, then R : r is equal to
In a right angled triangle R is equal to
If the area of triangle is 100 sq. cm, r1 = 10 cm and r2 = 50 cm, then the value of (b – a) is equal to
In a ΔABC, the inradius and three exradii are r, r1, r2 and r3 respectively. In usual notations the value of r . r1 . r2 . r3 is equal to
The product of the arithmetic mean of the lengths of the sides of a triangle and harmonic mean of the lengths of the altitudes of the triangle is equal to
In a ΔABC, if AB = 5 cm, BC = 13 cm and CA = 12 cm, then the distance of vertex A from the side BC is (in cm)
If AD, BE and CF are the medians of ΔABC, then (AD2 + BE2 + CF2) : (BC2 + CA2 + AB2) is equal to
In a triangle ABC, right angled at B, the inradius is
If H is the orthocentre of a triangle ABC, then the radii of the circle circumscribing the triangles BHC, CHA and AHB are respectively equal to
The distance between the middle point of BC and the foot of the perpendicular form A is
Let f, g, h be the lengths of the perpendiculars from the circumcentre of the ΔABC on the sides a, b and c respectively. If a/f + b/g + c/h = l (abc/fgh) then the value of l is
In a triangle ABC, if =
, then r1, r2, r3 are in
A triangle is inscribed in a circle. The vertices of the triangle divide the circle into three arcs of length 3, 4 and 5 units. Then area of the triangle is equal to
If in a triangle ABC, the line joining the circumcentre and incentre is parallel to BC, then cos B + cos C is equal to
If the incircle of the ΔABC touches its sides respectively at L, M and N and if x, y, z be the circumradii of the triangles MIN, NIL and LIM where I is the incentre then the product xyz is equal to
If in a ΔABC, = , then the value of tan is equal to
If in a ΔABC, ∠A = , then tan C/2 is equal to
In a acute angled triangle ABC, AP is the altitude. Circle drawn with AP as its diameter cuts the sides AB and AC at D and E respectively, then length DE is equal to