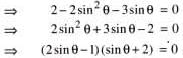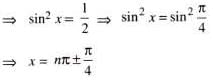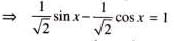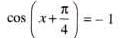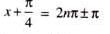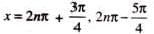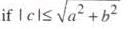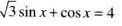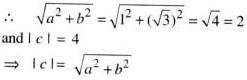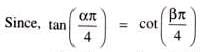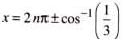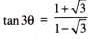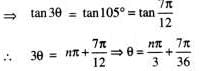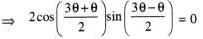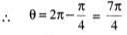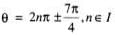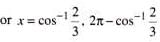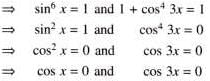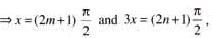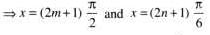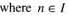Competition Level Test: Solution Of Triangles- 2 - JEE MCQ
30 Questions MCQ Test Additional Study Material for JEE - Competition Level Test: Solution Of Triangles- 2
If 2cos θ < √3 and x ∈ [-π,π] then the solution set for ‘x’ is
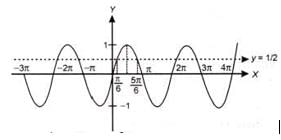
If 2 sin x + 1 > 0 and x ∈ [0, 2π] , then the solution set for x is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If cos x – sin x > 1 and 0 < x < 2π , then the solution set for x is
The number of values of x lying in the interval (-π, π) which satisfy the equation
The equation esin x - e-sin x - 4 = 0 has
If tan (π cos θ) = cot (π sin θ) , then the value(s) of
If the equation cos 3x + cos 2x = sin 3x/2 + sin x/2, 0 < x < 2π then the number of value of x is
The number of solutions of cos x.cos 2x.cos 3x = 1/4 in [0,π] is equal to
Total number of solutions of sin4 x + cos4 x = sin x. cos x in [0, 2π] is equal to
The number of solutions of the pair of equations 2 sin2 θ - cos2θ = 0 and 2 cos2 θ - 3sin θ = 0 in the interval [0, 2π] is
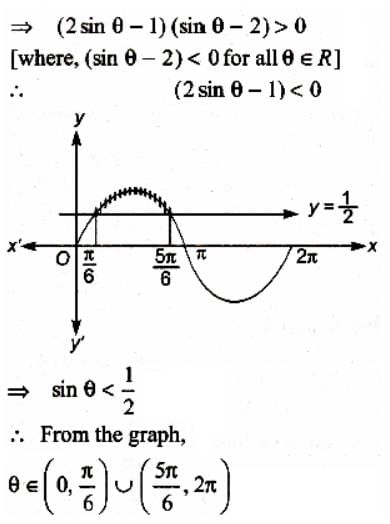
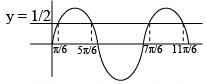
The set of values of q satisfying the inequation 2 sin2 θ - 5 sin θ + 2 > 0 , where 0 < θ < 2π is
The number of values of x in the interval [0, 3π] satisfying the equation 2 sin2 x + 5 sin x - 3 = 0 is
The solutions of the equation 4 cos2 x + 6 sin2 x = 5 are
The general solution of sin x - cos x = √2, for any integer n is
The equation √3 sin x + cos x = 4 has
The equation 3 sin2x + 10 cos x – 6 = 0 is satisfied, if
The number of solutions for the equation sin 2x + cos 4x = 2 is
If sin 3θ = sin θ, how many solutions exist such that -2π < θ <2π ?
The most general value of θ satisfying the equation sin θ = sin α and cos θ = cos α is
The general value of θ in the equation cos θ = 1/√2, tan θ = -1 is
The number of values of x in [0, 2π] satisfying the equation 3 cos 2x -10 cos x + 7 = 0 is
If sin6 x = 1 + cos4 3x, then x is equal to
If equation sin4x = 1 + tan8x, then x is
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|


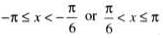
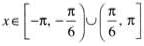
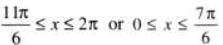
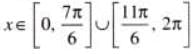

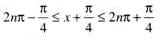
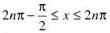
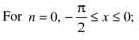
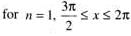
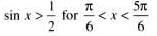
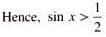
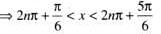
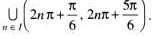
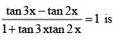
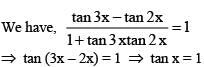
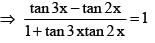
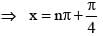
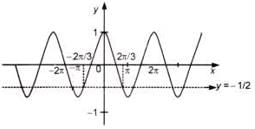
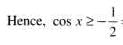
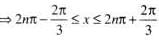


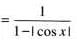
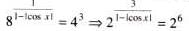
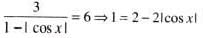

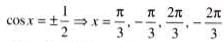
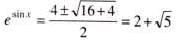
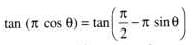
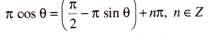
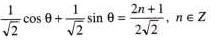
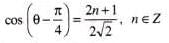
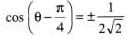


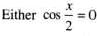
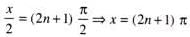
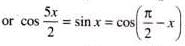

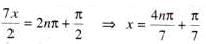

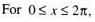
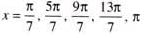
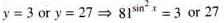
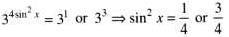
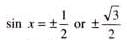
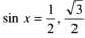

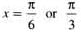
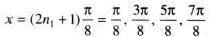
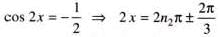
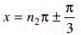
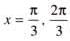
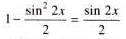
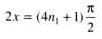
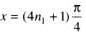
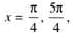
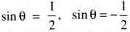 .......(1)
.......(1)