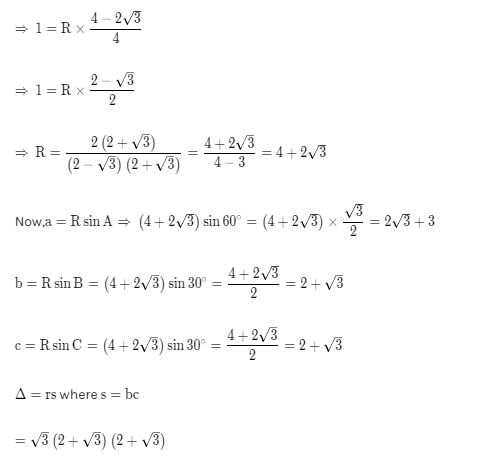Competition Level Test: Solution Of Triangles- 3 - Class 11 MCQ
27 Questions MCQ Test - Competition Level Test: Solution Of Triangles- 3
AA1, BB1 and CC1 are the medians of triangle ABC whose centroid is G. If points A, C1, G and B1 are concyclic, then
If l is the median from the vertex A to the side BC of a ΔABC, then
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a ΔABC, a = 1 and the perimeter is six times the A.M. of the sines of the angles. Then measure of ∠A is
If the median AD of a triangle ABC divides the angle ∠BAC in the ratio 1 : 2, then 
is equal to
In a triangle ABC, let ∠C = π/2, if r is the inradius and R is the circumradius of the triangle ABC, then 2(r + R) equals
If in a ∠ABC, the altitudes from the vertices A, B, C on opposite sides are in HP, then sinA, sinB, sinC are in
The sides of a triangle are sina, cosa, and 
for some 0 < a < π/2. Then the greatest angle of the triangle is
The sum of the radii of inscribed and circumscribed circle for an n sided regular polygon of side a, is
If in a triangle ABC a cos2
+ c cos2
=3b/2, then the sides a, b and c
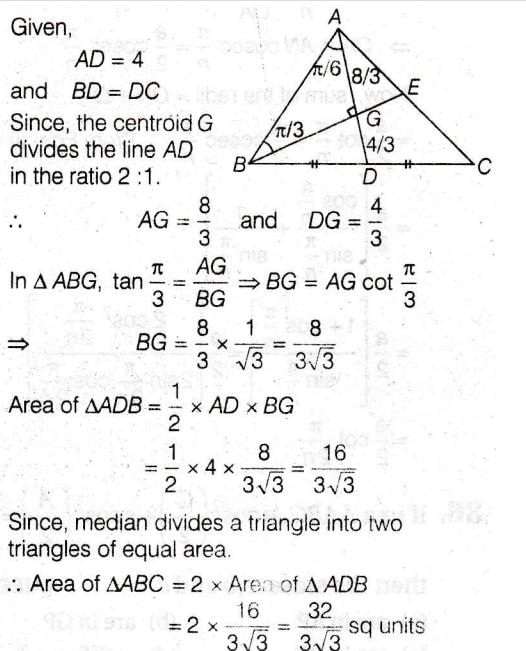
In a triangle ABC, medians AD and BE are drawn. If AD = 4, ∠DAB = π/6 and ∠ABE =π/3, then the area of the ΔABC is
If the radius of the circumcircle of an isosceles triangle PQR is equal to PQ = PR then the angle P is
Given an isosceles triangle, whose one angle is 120º and radius of its incircle is √3, then the area of the triangle in sq. units is
The sides a, b, c of a triangle ABC are the roots of x3 – 11x2 + 38x – 40 = 0, then 
=
In a triangle ABC 
= 4, ∠C = π/3, then a2 + b2 – c2 =
In a triangle cot A : cot B : cot C = 30 : 19 : 6, then a : b : c
If twice the square of the diameter of a circle is equal to sum of the squares of the sides of the inscribed triangle ABC, then sin2A + sin2B + sin2C is equal to
In a triangle ABC if a/1 = b/√3 = c/2, then
In a triangle ABC, if s – a, s – b, s – c are in GP, then 
=
, then ΔABC isIn a triangle ABC if 
= 
, then sin (B+C) is equal to
In a triangle ABC, 1 – tan (A/2) tan (B/2) is equal to
The angles of a triangle ABC are in A.P. The largest angle is twice the smallest angle and the median to the largest side divides the angle at the vertex in the ratio 2 : 3. If length of the median in 2√3 cm, length of the largest side is
The vertices angle of a triangle is divided into two parts, such that the tangent of one part is 3 times the tangent of the other and the difference of these parts is 30º, then the triangle is
In a triangle ABC, if tan (A/2) = p, tan (B/2) = q, then 
is equal to
If I is the incentre of a triangle whose in raidus and circumradius are r and R respectively; I1 I2 I3 is its ex-centre triangle, then I I1 . I I2 . I I3 is equal to
If R is the circumradius of a triangle ABC then the area of its pedal triangle is
In an isosceles triangle with base angle a and lateral side 4, Rr =
Top Courses for Class 11
Important Questions for Competition Level Test: Solution Of Triangles- 3
Competition Level Test: Solution Of Triangles- 3 MCQs with Answers
Online Tests for Competition Level Test: Solution Of Triangles- 3
|
© EduRev
|
Education Revolution
|
|
