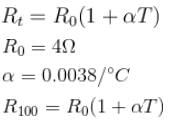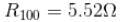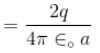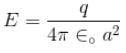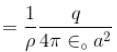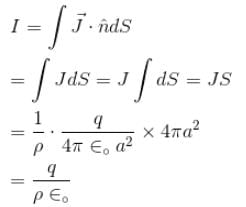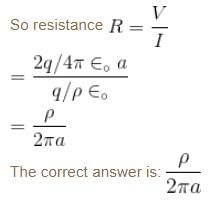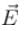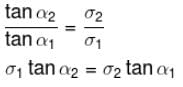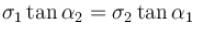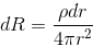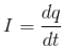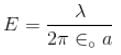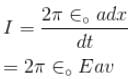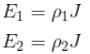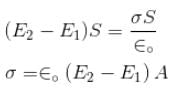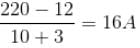Courses
Get the App Signup / Login

Current Electricity MCQ Level - 3


10 Questions MCQ Test Basic Physics for IIT JAM | Current Electricity MCQ Level - 3


Description
This mock test of Current Electricity MCQ Level - 3 for Physics helps you for every Physics entrance exam. This contains 10 Multiple Choice Questions for Physics Current Electricity MCQ Level - 3 (mcq) to study with solutions a complete question bank. The solved questions answers in this Current Electricity MCQ Level - 3 quiz give you a good mix of easy questions and tough questions. Physics students definitely take this Current Electricity MCQ Level - 3 exercise for a better result in the exam. You can find other Current Electricity MCQ Level - 3 extra questions, long questions & short questions for Physics on EduRev as well by searching above.
QUESTION: 1

The resistance of platinium wire at 0°C is 4Ω  What will be the resistance of the wire at 100°C. If the temperature coefficient of resistance of platinium is 0.0038/°C

Solution:

We know, Resistance depend on temperature by relation.

R100 = 4(1 + 0.0038 × 100)
R100 = 4(1 + 0.38)

The correct answer is: 5.52Ω

QUESTION: 2

Two metal ball of the same radius a  are located in homogeneous poorly conducting medium with resistivity ρ.The resistance of the medium between the ball provided that the separation between them is much greater than the radius of the ball.

Solution:

Let us impart charge  q  and  –q  to the balls respectively. Potential difference between two balls

V = V+ – V–

Electric field at the surface of first sphere

electric field due to second sphere at the surface of first sphere is negligible
current density J = σE

The electric current

QUESTION: 3

In case of insulator as the temperature decrease resistivity

Solution:

The correct answer is: Increases

QUESTION: 4

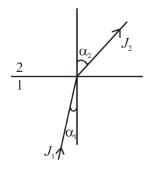
The law of refraction of direct current lines at the boundary between two conducting media having  σ1 and σ2  are the conductivity of media 1 and 2 and  α1 and α2 are the angle between the current lines and normal of the boundary surface as shown in figure.
Solution:

Applying boundary condition of 

Dividing (2) by (1)

The correct answer is: 

QUESTION: 5

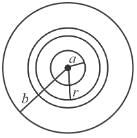
A metal ball of radius a  is surrounded by a thin concentric metal shell of radius b. The space between these electrodes is filled up with a poorly conducting homogeneous medium of resistivity ρ. The resistance of the interelectrode gap. assume  b → ∞
Solution:

As the current flow from inner to outer shell, the cross-section area increase. Assuming an element in form of spherical shell of radius r  and thickness  dr

The resistance

Net resistance

QUESTION: 6

A long cylinder with uniformly charged surface an cross-section radius a  moves with a constant velocity v  along its axis. An electric field strength at the surface of the cylinder is equal to  E. So current caused by mechanical transfer of a charge.
Solution:

The convection current is

Here, dq = λdx. where λ is the linear charge density. But, from the gauss, theorem, electric field at the surface of the cylinder,

Hence, substituting the value of λ and subsequently of dq  in Equation (i), we get

The correct answer is: 

QUESTION: 7

What is the drift velocity of an electron in a copper conductor having area 10 × 10–6 m2 and 10 × 1028 electron/m3
Solution:

We know, current through conductor = I = neAvd
where A = Area
vd = drift velocity
e = charge on electron
n = number of electron per unit volume

The correct answer is: 1.25 × 10–5 m/s

QUESTION: 8

Two cylindrical conductor with equal cross-sections and different resistivity  ρ1 and ρ2 are put end to end. The charge at the boundary of the conductor if a current I flows from conductor 1 to conductor 2
Solution:

The current density

J = I/A

Electric field in the two conductor are given by

If we consider of Gaussian pill box of cross-section area S at the interface of two conductors.

The flux of 

According to Gauss Law

where σ  is the surface charge density at the interface

So, charge at the boundary of two conductors

The correct answer is: 

QUESTION: 9

A current of 1A flows through a copper wire. How many electron pass through any cross-section of the wire in 1.6 seconds. (Charge on electron in 1.6 × 10–19C)
Solution:

I = 1A
t = 1.6 second

⇒ q = It = 1 × 1.6 = 1.6
q = 1.6C
q = ne
n = number of electrons

The correct answer is: 1019

QUESTION: 10

A battery of 6 cells, each of emf 2V and internal resistance 0.5Ω is being charged by a 220V  supplying  an external resistance of 10Ω is series. The potential difference across the battery is :
Solution:

Total emf of the battery = 12 V
Total internal resistance of the battery = 3Ω

Current through battery (I) = 
Potential difference across battery  = emf of battery + Potential across the battery = 12 + (16 × 3)
= 60 V
The correct answer is: 60 V

Recommended Content

Recommended Tests

Related tests
Follow Us
© EduRev