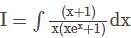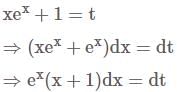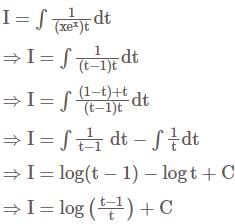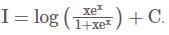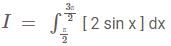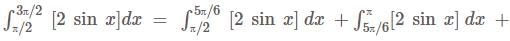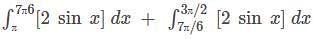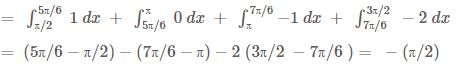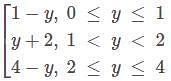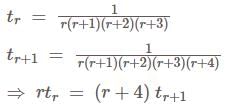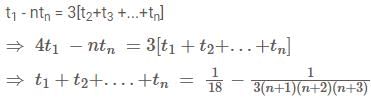DSSSB TGT Mathematics Mock Test - 1 - DSSSB TGT/PGT/PRT MCQ
30 Questions MCQ Test - DSSSB TGT Mathematics Mock Test - 1
"To develop new theories by discovering broad generalisations" is the purpose of
Who applied the concept of action research 'J first time
Appropriate method for the establishment of the formulae in mathematics is
In the text-book of mathematics, the content should be developed
The most suitable definition of mathematics may be given as
In △ABC, ∠B = 90º and D is a point on BC such that AD is the bisector of ∠A. If AB = 12 cm and BC = 9 cm, then find the length of CD:
The greatest positive integer, which divides n (n + 1) (n + 2) (n + 3) for all n ∈ N is
When a number is divided by 3 it leaves remainder as 2. What will be the remainder when 3n + 6 is divided by 3?
The number of ways so that the birthdays of 6 people falls in exactly 3 calendar months is
Let P(n) be the statement 2n < n!, where n is a natural number. Then, P(n) is true for
The equation of line which passes through the point of intersection of 2x + 3y – 5 = 0 and x + y = 2 and also which is farthest from (2, 3) is
The diagonals of a parallelogram PQRS are along the lines x + 3y = 4 and 6x – 2y = 7. Then PQRS must be
The complete set of values of m for which the function
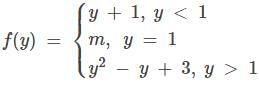 is strictly increasing at y =1
is strictly increasing at y =1
Find the component of in the direction of the vector 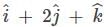
The function f(x) 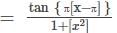 where [x] denotes the greatest integer less than or equal to x, is
where [x] denotes the greatest integer less than or equal to x, is
Let f(y) be defined in the interval [0,4] such that 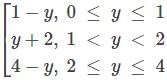 then the number of points where f(f(yy)) is discontinuous is
then the number of points where f(f(yy)) is discontinuous is
If P(n) = 2 + 4 + 6 + ........ + 2n, n ∈ N, then P(k) = k(k + 1) + 2 ⇒ P(k + 1) = (k + 1)(k + 2) + 2 for all k ∈ N. So, we can conclude that P(n) = n(n + 1) + 2 for
The range of the following functions defined over [0, 3] and is given by
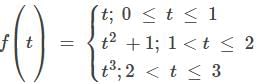



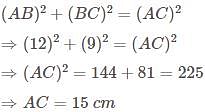
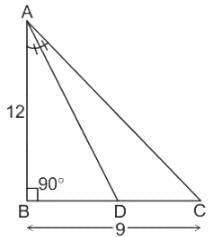
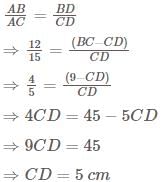

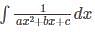 then replace ax2 +bx + x by
then replace ax2 +bx + x by

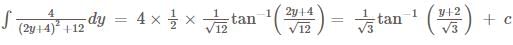
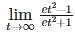
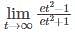
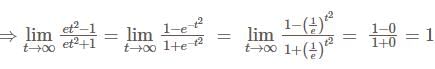

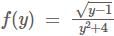
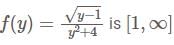
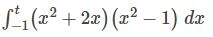
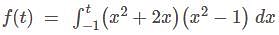
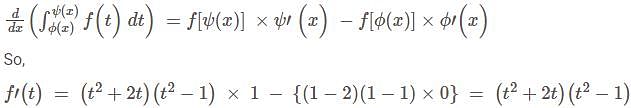
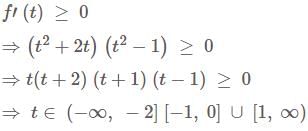
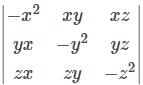
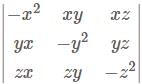
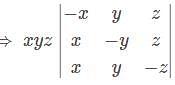
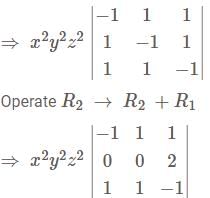
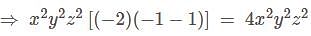
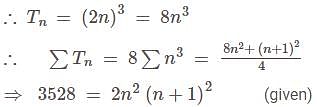


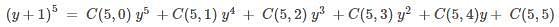
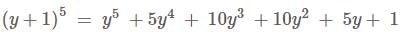
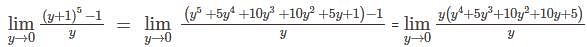
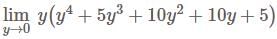
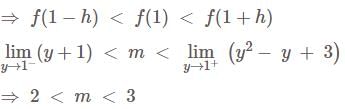
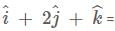 projection of
projection of 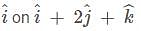
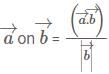

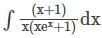 is equal to:
is equal to: