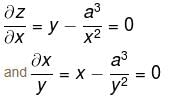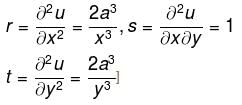Differential Calculus NAT Level - 1 - IIT JAM MCQ
10 Questions MCQ Test - Differential Calculus NAT Level - 1
If f"(x) > 0 and f'(1) = 0 such that g(x) = f(cot2 x + 2cot x + 2) where 0 < x < π, then g(x) decreasing in (a, b) where 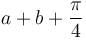 is
is
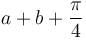 is
isIf f(x) has a maximum or a minimum at a point x0 inside the interval, then f '(x0) equals :
If 1" = α radians, then the approximate value of cos 60°1' is given as 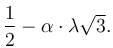 Find the value of λ.
Find the value of λ.
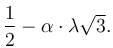 Find the value of λ.
Find the value of λ.The maximum value of u is, where u = axy2z2 - x2y2z3 - xy3z3 - xy2z4 is 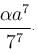 Find the value of α.
Find the value of α.
The sum of one number and three times a second number is 60. Find the pair, where product is maximum.
Let 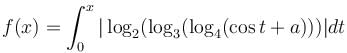 be increasing for all real values of x, then range of a is (α, ∞). Find value of α.
be increasing for all real values of x, then range of a is (α, ∞). Find value of α.
The greatest and the least value of the function f(x) = x3 – 18x2 + 96x in the interval [0, 9] are :
Let f(x, y) = x4 + y4 - 2x2 + 4xy - 2y2 has a minimum at (-√α, √α) and (√α, - √α) Find the value of α.
If the function 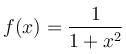 is downward concave is (α, β) the [β - α] is
is downward concave is (α, β) the [β - α] is


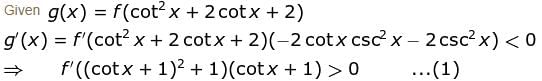
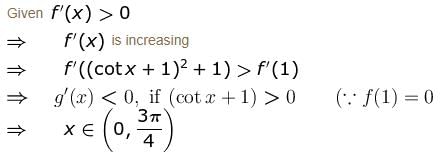
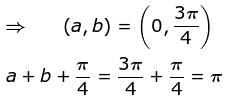

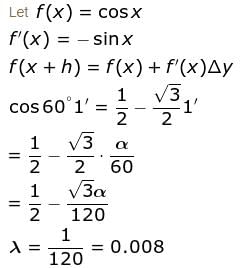

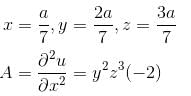

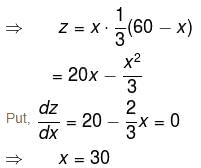
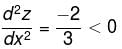

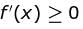
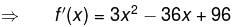
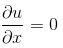
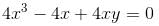
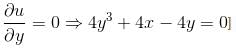
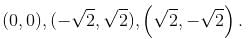
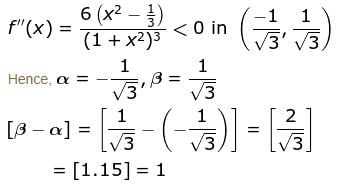
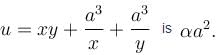 Find the value of α.
Find the value of α.