Differential Calculus NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Differential Calculus NAT Level - 2
Maximum area of a rectangle which can be inscribed in a circle of given radius R is given by αR2. Find the value of α.
The radius of a right circular cylinder increases at a constant rate. Its altitude is a linear function of the radius and increases three times as fast as radius. When the radius is 1 cm the altitude is 6 cm. When the radius is 6 cm, the volume is increasing at the rate of 1 cm/s. When the radius is 36 cm, the volume is increasing at a rate of n cm3/s. The value of 'n' is equal to :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The maximum value of 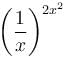 is given as (λ/e). The value of λ is
is given as (λ/e). The value of λ is
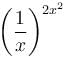 is given as (λ/e). The value of λ is
is given as (λ/e). The value of λ isConsider the function 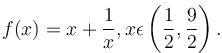 If α is the length of interval of decrease and β be the length of interval of increase, then β/α is
If α is the length of interval of decrease and β be the length of interval of increase, then β/α is
If the interval of monotonicity of the function 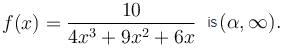 Find the value of α?
Find the value of α?
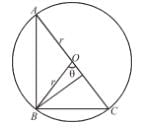
The least area of a circle circumscribing any right triangle of area S is given as απS. Find the value of α.
Let f(x) = 2x3 + ax2 + bx - 3cos2 x is an increasing function for all x∈R such that ma2 + nb + 18 < 0 then the value of m + n + 7 is
If the maximum value of the function f(x) = (sin-1 x)3 + (cos-1 x)3, -1 < x < 1 is α and minimum value is β and α - β is of the form n · π3. Find the value of n.
If a, b, c, d are real numbers such that 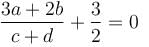 then the equation ax3 + bx2 + cx + d = 0 has at least one root in (0, α). Find the value of α.
then the equation ax3 + bx2 + cx + d = 0 has at least one root in (0, α). Find the value of α.


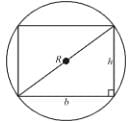
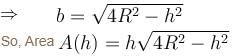
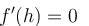
 = h2(–2h) + (4R2 – h2)2h = 0
= h2(–2h) + (4R2 – h2)2h = 0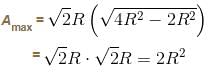
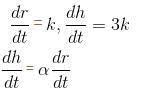
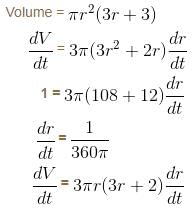
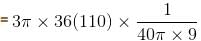
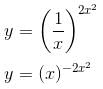
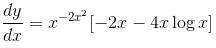
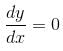
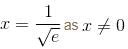
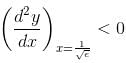
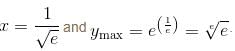
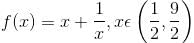
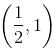 and increasing in
and increasing in 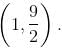
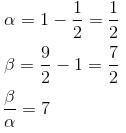
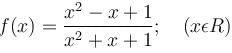 is
is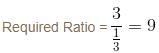
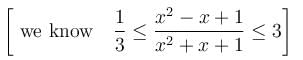
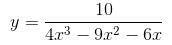
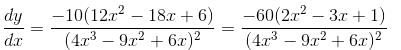
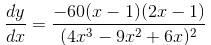
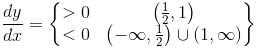
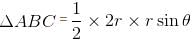
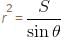
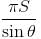
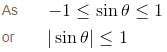
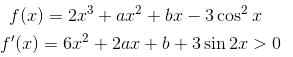
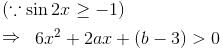
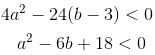

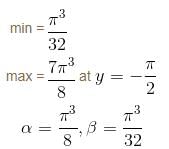
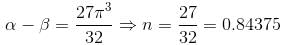
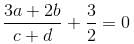
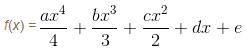
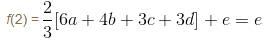
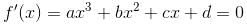 has at least one root in (0,2). Thus, value of α = 2.
has at least one root in (0,2). Thus, value of α = 2.














