Electric Potential MCQ (With Solution) : Test 2 - Class 12 MCQ
25 Questions MCQ Test - Electric Potential MCQ (With Solution) : Test 2
An electric field is expressed as 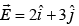 . Find the potential diference (VA-VB) between two points A and B whose position vectors are given by
. Find the potential diference (VA-VB) between two points A and B whose position vectors are given by 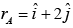 and
and 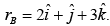
The potential function of an electrostatic field is given by V = 2x2. Determine the electric field strength at the point (2 m, 0.3 m).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
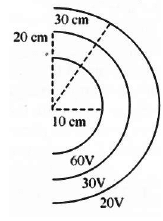
Figure 3.79 shows equipotential surfaces concentric at O, the magnitude of electric field at a distance r measured from O is
The electric field in a certain region is A/x3. Then the potential at a point (x,y, z), assuming the potential at infinity to be zero, is
Find the potential V of an electrostatic field , where a is constant.
Consider a system of three charge q/3,q/3 and -2q/3 placed at points A,B and C, respectively, as shown in figure. Take O to be the circle of radius R and angle CAB = 60°.
Two equal positive charges are kept at points A and B.The electric potential at the points between A and B (excluding these points) is studied while moving from A to B. The potential
Figure shows three paths along which we can move positively charged sphere A closer to positively charged sphere B which is fixed in a plane. if W1, W2 and W3 are the work done along the three respective paths, then
The work done in moving an electron of charge e and mass m from A to B along the circular path (shown in figure) in the vertical plane in the field of charge Q is
Four similar point charges q are located at the vertices of a tetrahedron with an edge a. The energy of the interaction of charges is :
In the electric field of a point charge q, a certain charge is carried from point A to B, C, D and E. Then the work done
Four equal charges Q are placed at the four corners of a square of each side is a. Work done in removing a charge -Q from its centre of infinity is
Ten electrons are equally spaced and fixed around a circle of radius R. Relative to V = 0 at infinity, the electrostatic potential V and the electric field E at the centre C are
The displacement of a charge Q in the electric field . The work done is
Three charges Q + q and +q are placed at the vertices of a right-angled isosceles triangle as shown. The net electrostatic energy of the configuration is zero if Q is equal to
Electric potential at any point is V = - 5x +3y + √15z, then the magnitude of the electric field is
Equipotential surfaces associated with an electric field which is increasing in magnitude along the x-direction are.
Figure shown three points A,B and C in a region of uniform electric field The line AB is perpendicular and BC is parallel to the field lines. Then which of the following holds good. Where VA, VB and VC represent the electric potential at points A,B and C respectively
A charge +q is fixed at each of the points x = x0, x = 3x0, x = 5x0....... infinite, on the x-axis and a charge -q is fixed at each of the points x = 2x0, x = 4x0, x = 6x0..... infinite. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be . Then, the potential at the origin due to the above system of charges is
A non-conducting ring of radius 0.5 m carries a total charge of 1.11×10-10C distributed non-uniformly on its circumference producing an electric field everywhere in space. The value of the line integral
being centre of the ring) in volts is
A charged particle q is shot towards another charged particle Q which is fixed, with a speed v. It approaches Q upto a closest distance r and then returns. if q were given a speed 2v, the closest distances of approach would be
The electric potential at a point distant r from an electric dipole is proportional to
In the electric field of a point charge q shown, a charge is carried from A to B and from A to C. Compare the work done
The potential at a point x (measured in µm) due to some charges situated on the X-axis is given by
The electric field E at x = 4 µm is given by :
The electric potential at a point (x,y,z) is given by tential at a point (x,y,z) is given by V = x2 y - xz3 + 4
The electric field at that point is :

















