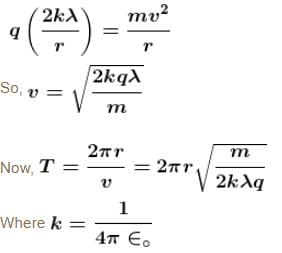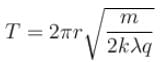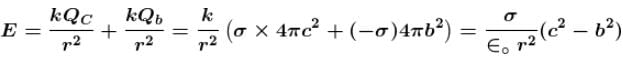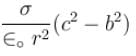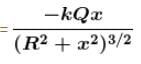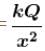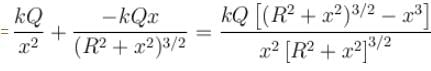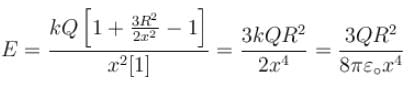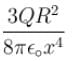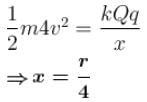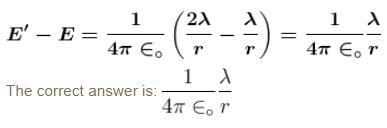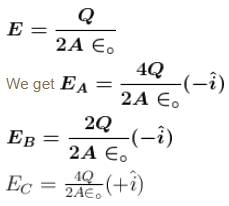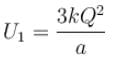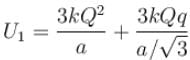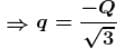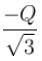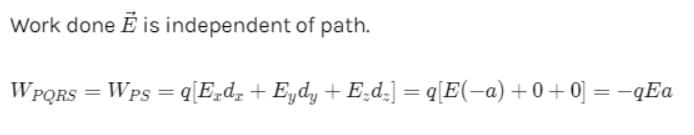Electrostatics MCQ Level - 1 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Electrostatics MCQ Level - 1
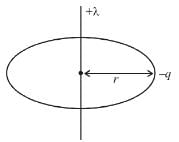
A particle of charge –q and mass m moves in a circle of radius r around an infinitely long line charge on linear charge density +λ. Then time period will be :
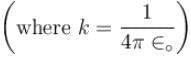
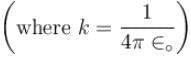

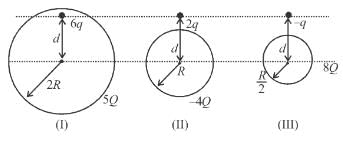
Figure, shown above shows three situations involving a charged particle and a uniformly charged spherical shell. The charges and radii of the shells are indicated in the figure. If F1, F2 and F3 are the magnitudes of the force on the particle due to the presence of the shell in situations (I), (II) and (III) respectively then

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
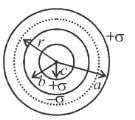
There are three concentric thin spheres of radius a, b, c (a > b > c). The total surface charge densities on their surfaces are σ, - σ, σ respectively. The magnitude of electric field at r (distance from centre) such that a > r > b is
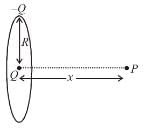
A point charge Q is located at centre of a fixed thin ring of radius R with uniformly distributed charge –Q. The magnitude of the electric field strength at the point lying on the axis of the ring at a distance x from the centre is
(x >> R)
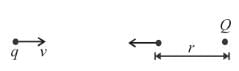
A charged particle q is shot towards another charged particle Q which is fixed, with a speed v. It approaches Q upto a closest distance r and then returns. If q was given a speed 2v, the closest distance of approach would be :
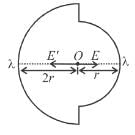
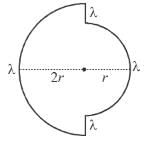
Two semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is
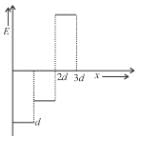
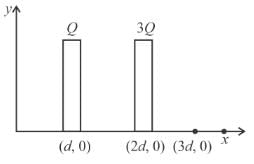
Two very large thin conducting plates having same cross sectional area are placed as shown in figure they are carrying charges Q and 3Q respectively. The variation of electric field as a function at x (for x = 0 to x = 3d) will be best represented by
Three equal charges Q are placed at the three vertices of an equilateral triangle. What should be the value of a charge, then when placed at the centroid, reduces the interaction energy of the system is zero :
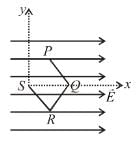
A point charge q moves from point P along the path PQRS (figure) in a uniform electric field E pointing parallel to the positive direction of the X-axis. The co-ordinates of points P, Q, R and S are (a, b, 0), (2a, 0, 0) (a, -b, 0), (0, 0, 0) respectively. The work done by the field in the above process is :
Four positive charges 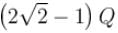 are arranged at corner of a square. Another charge q is placed at the centre of the square. Resultant force acting on each corner is zero if q is :
are arranged at corner of a square. Another charge q is placed at the centre of the square. Resultant force acting on each corner is zero if q is :