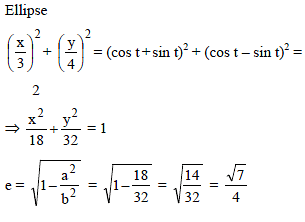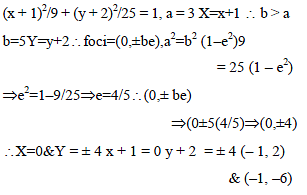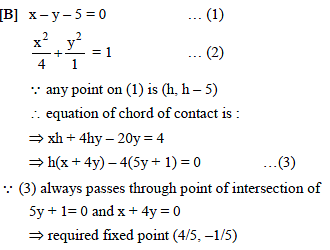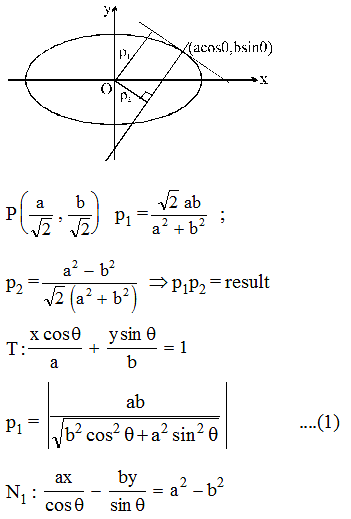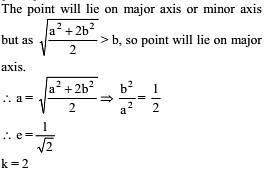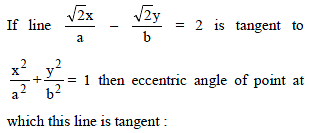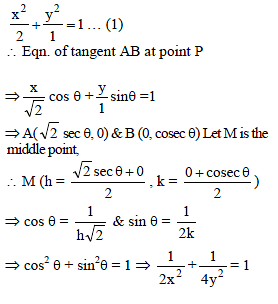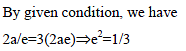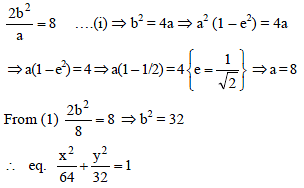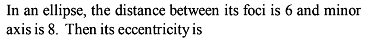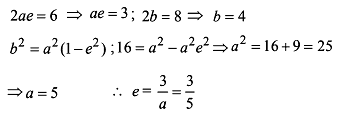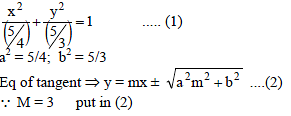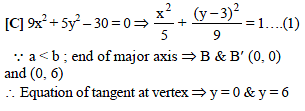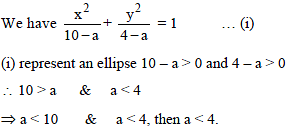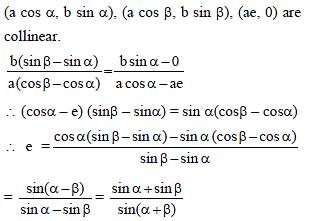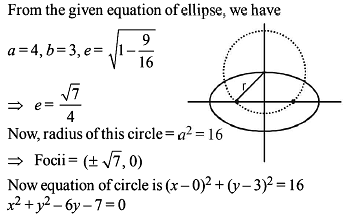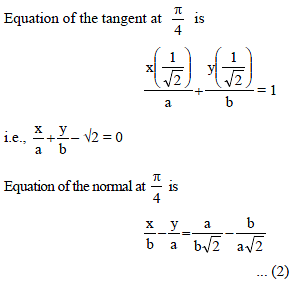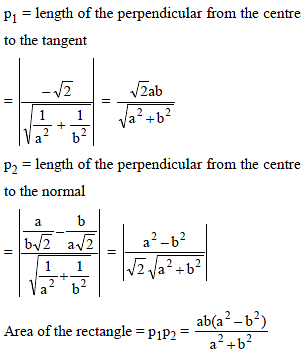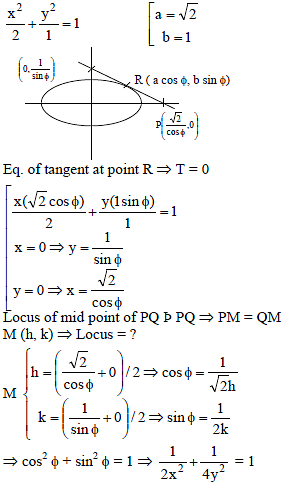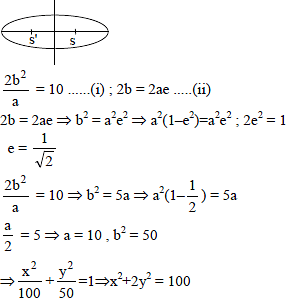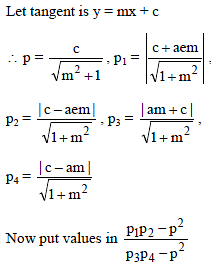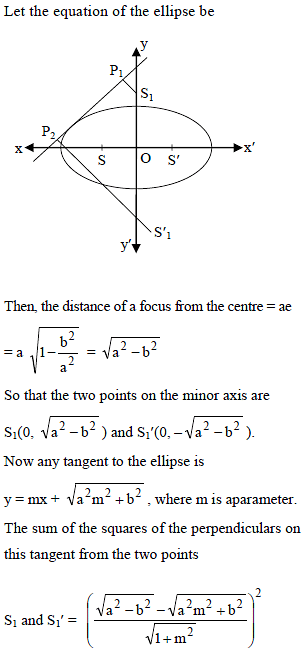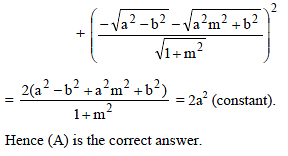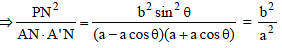Ellipse - 2 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Ellipse - 2
Eccentricity of ellipse whose equation is x = 3(cos t + sin t) , y = 4(cos t – sin t) where t is parameter :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Tangents are drawn from the points on the line x – y – 5 = 0 to x2 + 4y2 = 4, then all the chords of contact pass through a fixed point, whose co-ordinates are -
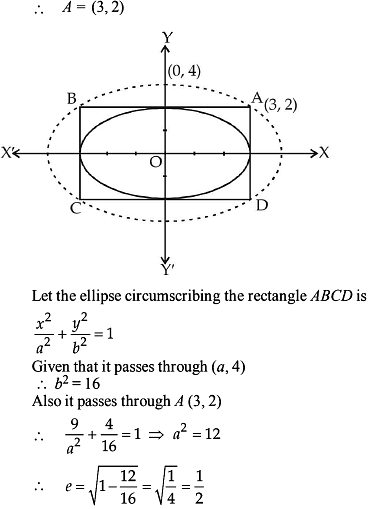
The area of the rectangle formed by the perpendiculars from the centre of the standard ellipse to the tangent and normal at its point whose eccentric angle is p/4 is :
If the focal distance of an end of the minor axis of any ellipse (its axes as x and y axis respectively) is k and the distance between the foci is 2h, then its equation is-
The locus of the middle point of the intercept of the tangents drawn from an external point to the ellipse x2 + 2y2 = 2 between the coordinates axes, is-
If the distance between directrices is thrice the distance between focii of an ellipse, then its eccentricity is -
The equation of the tangents to the ellipse 4x2 + 3y2 = 5 which are parallel to the line y = 3x + 7 are
The equation of the tangents drawn at the ends of the major axis of the ellipse 9x2 + 5y2 – 30y = 0, are-
If α, β are the eccentric angles of the extremities of a focal chord of an ellipse, then the eccentricity of the ellipse is -
If tangents are drawn to the ellipse x2 + 2y2 = 2, then the locus of the mid-point of the intercept made by the tangents between the co-ordinate axes is –
If minor axis of an ellipse is equal to the distance between foci and length of latus rectum is 10, the equation of the ellipse will be-
If two points are taken on the minor axis of an ellipse at the same distance from the center as the foci, then the sum of the squares of the perpendicular distances from these points on any tangent to the ellipse is -
PQ is a double ordinate of the ellipse x2 + 9y2 = 9, the normal at P meets the diameter through Q at R, then the locus of midpoint of PR is–
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|