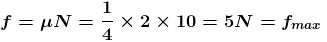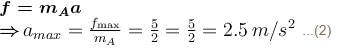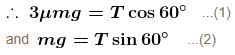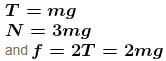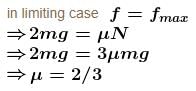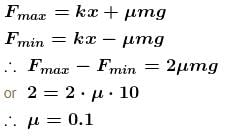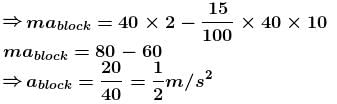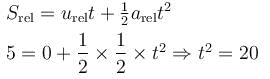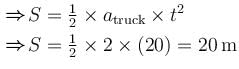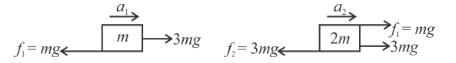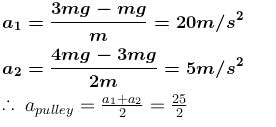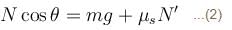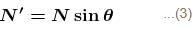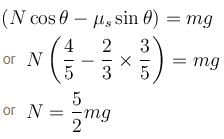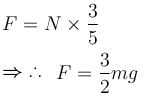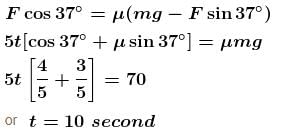Friction Force NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Friction Force NAT Level - 2
A 1.5kg box is initially at rest on a horizontal surface when at t = 0 a horizontal force 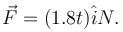 (with t in seconds), is applied to the box. The acceleration of box as a function of time t is given by :
(with t in seconds), is applied to the box. The acceleration of box as a function of time t is given by :
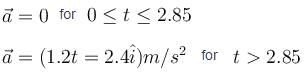
The coefficient of kinetic friction between the box and the surface is :
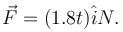 (with t in seconds), is applied to the box. The acceleration of box as a function of time t is given by :
(with t in seconds), is applied to the box. The acceleration of box as a function of time t is given by :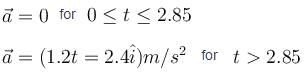
The coefficient of kinetic friction between the box and the surface is :
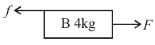
In figure shown, the coefficient of static friction between C and ground is 0.5, coefficient of static friction between A and B is 0.25, coefficient of static friction between B and C is zero. Find the minimum value of force F (is Newton), to causes sliding between A and B. Masses of A, and C are respectively 2kg, 4kg and 5kg.


| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
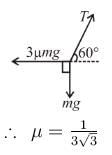
A mass m is supported as shown in the figure by ideal strings connected to a rigid wall and to a mass 3m at rest on a fixed horizontal surface. The string connected to larger mass is horizontal, that connected to smaller mass is vertical and the one connected to wall makes an angle 60° with horizontal. Then the minimum coefficient of static friction between the larger mass and the horizontal surface that permits the system to remain in equilibrium in the situation shown is given by 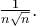
Find the value of n.
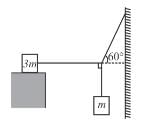

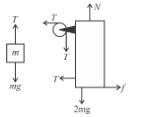
In the system shown in figure the friction coefficient between ground and bigger block is μ. There is no friction between both the blocks. The string connecting both the block is light; all three pulleys are light and frictionless. Then the minimum limiting value of μ so that the system remains in equilibrium is :
A block of mass 1 kg is placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x. 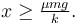 Let Fmax and Fmin be the maximum and minimum value of force F for which the block remains in equilibrium.
Let Fmax and Fmin be the maximum and minimum value of force F for which the block remains in equilibrium.
For a particular x, Fmax – Fmin = 2N. Also shown is the variation of Fmax + Fmin versus x, the elongation of the spring.
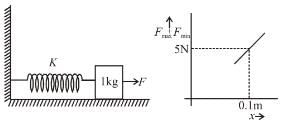
The coefficient of friction between the block and the horizontal surface is :
The rear side of a truck is open and a box of 40kg mass is placed 5m away from the open and as shown. The coefficient of friction between the box and the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with 2ms–2. At what distance (in m.) from the starting point does the box fall off the truck (i.e. distance traveled by the truck)? [Ignore the size of the box]
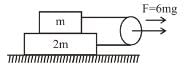
A block of mass m is placed on top of a block of mass 2m which in turn is placed on fixed horizontal surface. The coefficient of friction between all surfaces is µ = 1. A massless string is connected to each mass and wraps halfway around a massless and frictionless pulley, as shown in the figure. The pulley is pulled by horizontal force of magnitude F = 6mg towards right as shown. If the magnitude of acceleration of pulley is x/2 m/s2. Fill the value of x. (Take g = 10 m/s2)
A block of mass 5kg is placed on a rough horizontal surface of a moving compartment. It is seen by an observer sitting inside the compartment, that a force of 10N is required in horizontal direction to move the box in a direction parallel to the motion of compartment. While a force of 20N is required in horizontal direction to move the box in opposite direction. If coefficient of friction between the block and the surface is x/10 then find out value of x.
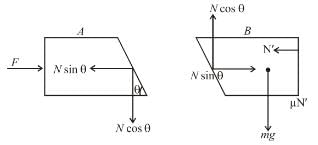
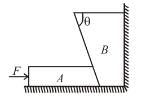
In the figure shown, the coefficient of static friction between B and the wall is 2/3 and the coefficient of kinetic friction between B and the wall is 1/3. Other contacts are smooth. Find the minimum force F required to lift B, up. It is 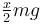 then x is. Mass of A is 2m and the mass of B is m. Take tan θ = 3/4.
then x is. Mass of A is 2m and the mass of B is m. Take tan θ = 3/4.
A block of 7 kg is placed on a rough horizontal surface and is pulled through a variable force F (in N) = 5t, where t is time is second, and an angle of 37° with the horizontal as shown in figure. The coefficient of static friction of the block with the surface is one. If the force starts acting at t = 0 s. Find the time (in sec.) at which the block starts to slide. (Take g = 10 m/s2) :