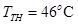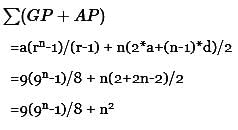GATE Numerical Computation Aptitude (Quant) Questions - 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - GATE Numerical Computation Aptitude (Quant) Questions - 2
A train that is 280 metres long, travelling at a uniform speed, crosses a platform in 60 seconds and passes a man standing on the platform in 20 seconds. What is the length of the platform in metres?
The sum of eight consecutive odd numbers is 656. The average of four consecutive even numbers is 87. What is the sum of the smallest odd number and second largest even number?
A man can row at 8 km per hour in still water. If it takes him thrice as long to row upstream, as to row downstream, then find the stream velocity in km per hour.
A batch of one hundred bulbs is inspected by testing four randomly chosen bulbs. The batch is rejected if even one of the bulbs is defective. A batch typically has five defective bulbs. The probability that the current batch is accepted is _________
A car travels 8 km in the first quarter of an hour, 6 km in the second quarter and 16 km in the third quarter. The average speed of the car in km per hour over the entire journey is
You are given three coins: one has heads on both faces, the second has tails on both faces, and the third has a head on one face and a tail on the other. You choose a coin at random and toss it, and it comes up heads. The probability that the other face is tails is
It takes 30 minutes to empty a half-full tank by draining it at a constant rate. It is decided to simultaneously pump water into the half-full tank while draining it. What is the rate at which water has to be pumped in so that it gets fully filled in 10 minutes?
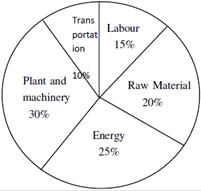
A firm producing air purifiers sold 200 units in 2012. The following pie chart presents the share of raw material, labour, energy, plant & machinery, and transportation costs in the total manufacturing cost of the firm in 2012. The expenditure on labour in 2012 is Rs. 4,50,000. In 2013, the raw material expenses increased by 30% and all other expenses increased by 20%. If the company registered a profit of Rs. 10 lakhs in 2012, at what price (in Rs.) was each air purifier sold?
In the summer of 2012, in New Delhi, the mean temperature of Monday to Wednesday was 41 °C and of Tuesday to Thursday was 43 °C. If the temperature on Thursday was 15% higher than that of Monday, then the temperature in °C on Thursday was
Find the sum to n terms of the series 10 + 84 + 734 + _____.



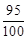
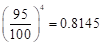
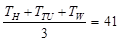 ...(1)
...(1)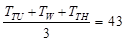 ...(2)
...(2)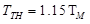 …(3)
…(3)