GATE Numerical Computation Aptitude (Quant) Questions - 1 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - GATE Numerical Computation Aptitude (Quant) Questions - 1
Operators □ , ◊ and → are defined by: 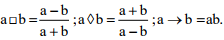 Find the value (66 □ 6) → (66◊6).
Find the value (66 □ 6) → (66◊6).
 Find the value (66 □ 6) → (66◊6).
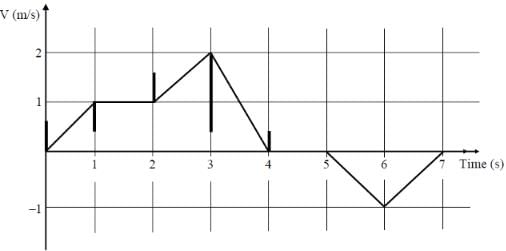
Find the value (66 □ 6) → (66◊6).The velocity V of a vehicle along a straight line is measured in m/s and plotted as shown with respect to time in seconds. At the end of the 7 seconds, how much will the odometer reading increase by (in m)?

log tan 1o + log tan 2o +.....+ log tan 89o is _____.
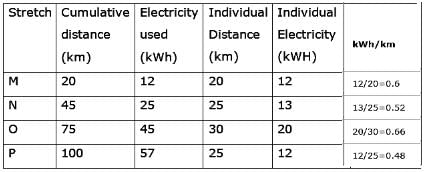
An electric bus has onboard instruments that report the total electricity consumed since the start of the trip as well as the total distance covered. During a single day of operation, the bust travels on stretches M, N, O and P, in that order. The cumulative distances traveled and the corresponding electricity consumption are shown in the Table below:
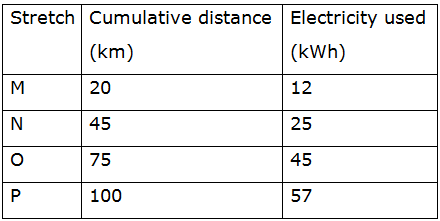
Q. The stretch where the electricity consumption per km is minimum is
If a2 + b2 + c2 = 1, then ab + ac + bc lies in the interval
The Venn diagram shows the preference of the student population for leisure activities.
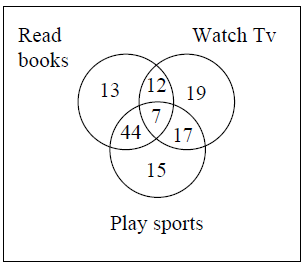
Q. From the data given, the number of students who like to read books or play sports is_____
If x > y > 1, which of the following must be true?
(i) ln x > ln y
(ii) ex > ey
(iii) y2 > x2
(iv) cos x > cos y
From a circular sheet of paper of radius 30cm, a sector of 10% area is removed. If the remaining part is used to make a conical surface, then the ratio of the radius and height of the cone is ________.
A tiger is 50 leaps of its own behind a deer. The tiger takes 5 leaps per minute to the deer’s 4. If the tiger and the deer cover 8 meters and 5 meters per leap respectively. What distance in metres will be tiger have to run before it catches the deer?
The statistics of runs scored in a series by four batsmen are provided in the following table:
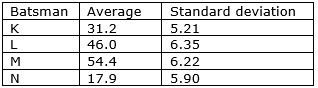
Q. Who is the most consistent batsman of these four?