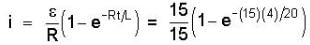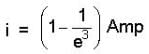GATE Physics Mock Test Series - 1 - Physics MCQ
30 Questions MCQ Test GATE Physics Mock Test Series 2025 - GATE Physics Mock Test Series - 1
Water from a tap emerges vertically down-wards with an initial speed of 1.0 m/ sec. The cross-sectional area of tap is 10-4m2. Assume that the pressure is constant throughout the stream of water and that the flow is steady, the cross-sectional area of stream 0.15 m below the tap is :
A vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300K. The ratio of the average rotational kinetic energy per O2 molecule to Per N2 molecule is :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Two particles each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitude of the magnetic moment of the system and its angular momentum about the centre of the rod is
Two identical containers A and B with frictionless pistons contain the same ideal gas at the same temperature and the same volume V. The mass of the gas in A is MA and that in B is MB. The gas in each cylinder is now allowed to expand isothermally to the same final volume 2V. The changes in the pressure in A and B are found to be MAΔ P and 1.5 MBΔ P respectively. Then
A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will be
If A denotes the area of free surface of a liquid and h is the depth of an orifice of area of cross-section a below the liquid surface then the velocity u of flow through the orifice is given by
A particle of mass 500 gm is at rest in the stationary reference frame. The motion of the particle with respect to reference frame rotating with an angular velocity 10π rad/sec2 is.
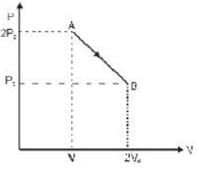
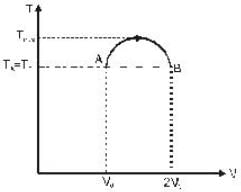
P-V diagram of n moles of ideal gas is as shown in figure. The maximum temperature between A and B is.
The half-life period of a radioactive element X is same as the mean lifetime of another radioactive element Y. Initially, both of them have the same number of atoms. Then:
Liquid oxygen at 50 K is heated to 300 K at constant pressure of 1 atm. The rate of heating in constant which of the following graphs represents the variation of temperature with time?
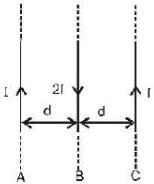
Consider three identical infinite straight wires A, B and C arranged in parallel on a plane as shown in the figure. The wires carry currents as shown in figure and have mass per unit length m. If the wires Aand C are held fixed and the wire B is displaced by a small distance x from its position, then it (B) will execute simple harmonic motion with a time period -
A thin conducting wire is bent into a circular loop of radius r and placed in a time dependent magnetic field of magnetic induction
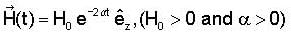
Such that, the plane of the loop is perpendicular to  Then the induced emf in the loop is
Then the induced emf in the loop is
Which one of the following curves gives the solution of the different at equation  where k1, k2 and k3, are positive constant with initial conditions x = 0 and t = 0 ?
where k1, k2 and k3, are positive constant with initial conditions x = 0 and t = 0 ?
A particle is in normalized state |ψ > which is a super position of the energy eigen states |E0 = 10eV > and |E1 = 30eV >. The average value of energy of the particle in the state | ψ > is 20eV. The state | ψ > is given by
Two beams A and B of plane polarized light with mutually perpendicular planes of polarization are seen through a polaroid. From the position when the beam A has maximum intensity (and Beam B has zero intensity) a rotation of polaroid through 60° makes the two beams appear equally bright. If the initial intensities of the two beams are lA and lB respectively, then  equals
equals
There are three sources of sound of equal intensity with frequencies 400, 401, and 402 vib/sec. The number of beats per second is
A wire of 9.8 *103 kg n-1 passes over a frictionless light pulley fixed on the top of a frictionless inclined plane which makes an angle of 30° with the horizontal. Masses m and M are tied at the two ends of wire such that m rests on the plane and M hangs freely vertically downwards. The entire system is in equilibrium and a transverse wave propagates along the wire with a velocity of 100 m/sec. Then the mass
In a test experiment on an aeroplane model in a wind tunnel flow, the speeds the air on the upper and lower surfaces of the wings are 70 m/sec and 63 m/sec respectively. If the area of the wings is 2.5 m2. then find the up thrust on the wings .
If the wave function ψ = X e -mωx2 /2ℏ and potential is defined as v = 1/2mω2x2 . Find out the eigen energy value of the particle.
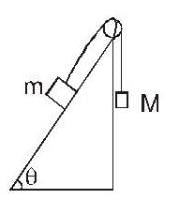
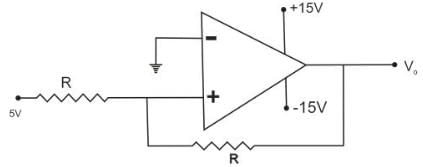
If the op-amp in the figure ; is ideal then V0 is :-
For a BJT, the current amplification factor “ a = 0.9” . This transistor is connected in CE configuration. When the base current changes by 0.4 mA, the change in collector current will be :-
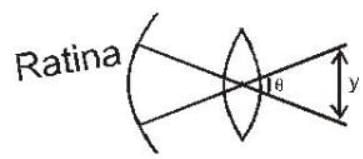
Assuming human pupil to have a radius of 0.25 cm and a comfortable viewing distance of 25 cm , the minimum separation between two objects that human eye can resolve at 500 nm wavelength is
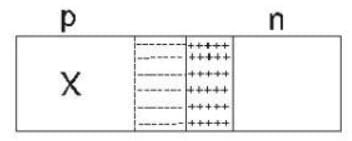
In the diagram of the space charge across a p-n junction as shown ; the region X has :-
For the three - particle system as shown is figure. Find the rotational interia about an axis perpendicular to the x - y plane and passing through the centre of mass of the system.
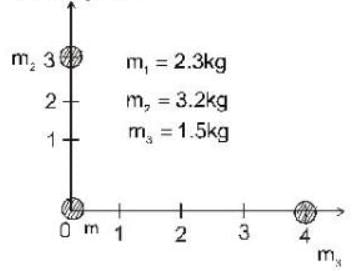
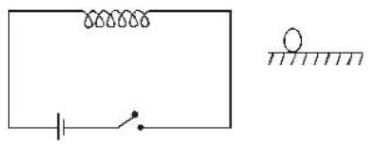
Figure shown a horizontal solenoid connected to a battery and a switch. A copper ring is placed on a frictionless, the axis of the ring being along the axis of the solenoid. As the switch is closed, the ring will :-
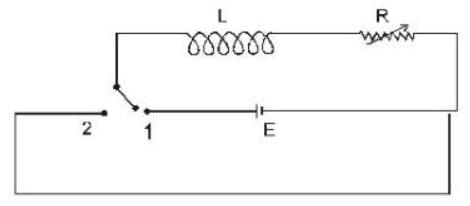
In the circuit shown in figure initially the switch is in position ‘1’ for a long time, then suddenly at t = 0, the switch is shifted to position ‘2’. It is required that a constant current should flow in the circuit, the value of Resistance ‘R’ in the circuit :-
In the circuit shown in figure L = 20 H, R = 15Ω, E = 15V, the switch ‘s’ is closed at t = 0. At t = 4 sec. The current in the circuit is : -
Two waves travel in the same direction along a string and interface. The waves have the same wavelength and travel with the same speed. The amplitude of each wave is 9.7 mm , and there is a phase difference of 110° between them. What is the amplitude of the combined wave resulting from the interface of the two waves ?
|
1 docs|34 tests
|


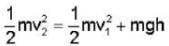
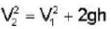
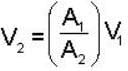
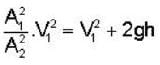
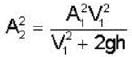

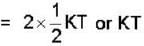
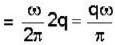

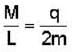

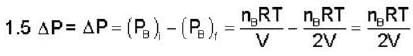

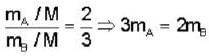
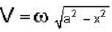
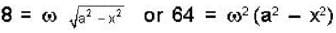
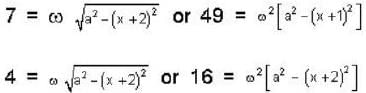
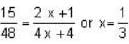

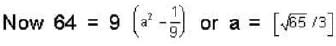
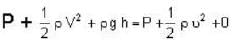 .....(1)
.....(1)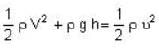
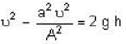

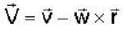
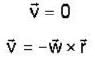
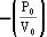 V + 3 P0 (y = - mx + c)
V + 3 P0 (y = - mx + c) 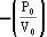 V2 + 3 P0V or nRT = 3 P 0V
V2 + 3 P0V or nRT = 3 P 0V 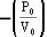 V2 (as PV = nRT)
V2 (as PV = nRT)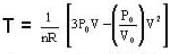
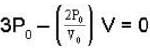
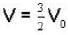
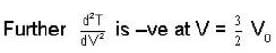
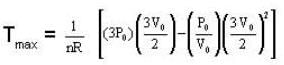
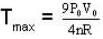
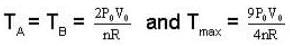
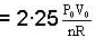

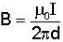
 towards right
towards right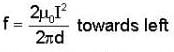
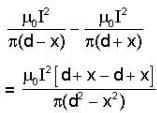
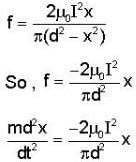
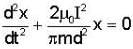
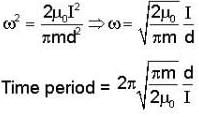

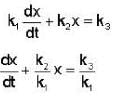

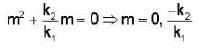
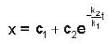
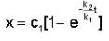
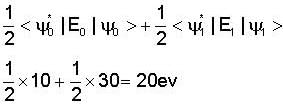
 ⇒ 2πt = 0 or 1 + 2 cos 2πt = 0
⇒ 2πt = 0 or 1 + 2 cos 2πt = 0 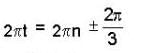

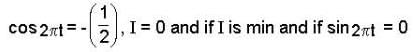
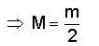

 M = 10kg, m = 20kg
M = 10kg, m = 20kg
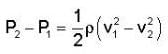


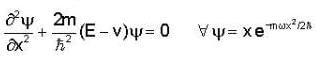
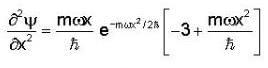

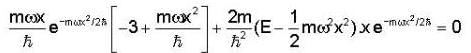
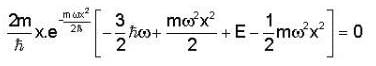
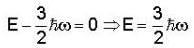
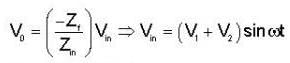
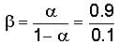

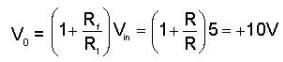
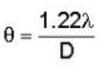
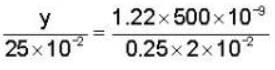
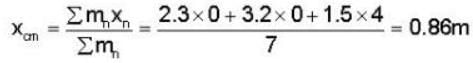

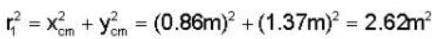

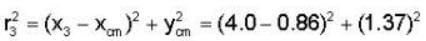
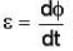 (because of lenz law).
(because of lenz law).