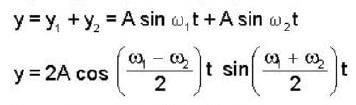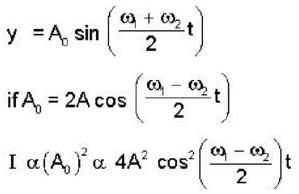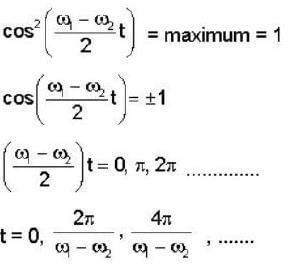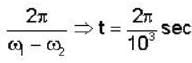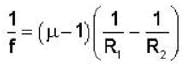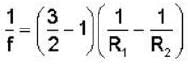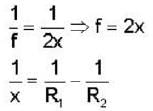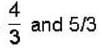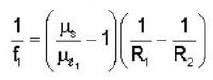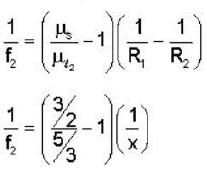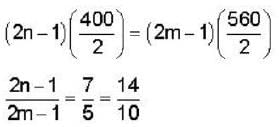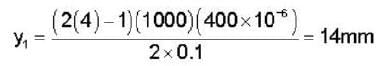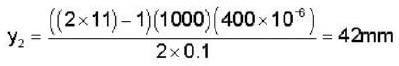GATE Physics Mock Test Series - 3 - Physics MCQ
30 Questions MCQ Test - GATE Physics Mock Test Series - 3
At what speed the volume of an object will shrinks to half its rest volume?
Calculate the energy released by 1 g of natural uranium assuming 200 MeV is released in each fission event and that the fissionable isotope 235U has an abundance of 0.7% by weight in natural uranium.
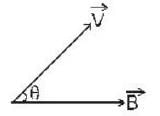
A charged particle of mass'm',charge 'q' and constant velocity 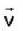 enters a uniform magnetic field
enters a uniform magnetic field 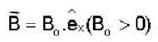 at an angle θ to the direction of magnetic field.The angle'θ'(if,one revolution of the helical motion,the particle advances along the direction of the magnetic field at a distance equal to the radius of the helical path) is:-
at an angle θ to the direction of magnetic field.The angle'θ'(if,one revolution of the helical motion,the particle advances along the direction of the magnetic field at a distance equal to the radius of the helical path) is:-
 enters a uniform magnetic field
enters a uniform magnetic field 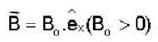 at an angle θ to the direction of magnetic field.The angle'θ'(if,one revolution of the helical motion,the particle advances along the direction of the magnetic field at a distance equal to the radius of the helical path) is:-
at an angle θ to the direction of magnetic field.The angle'θ'(if,one revolution of the helical motion,the particle advances along the direction of the magnetic field at a distance equal to the radius of the helical path) is:-A free particle is moving in positive direction with linear momentum (p) The wave function of the particle normalized in a length (L) is:-
Applying normalization, we get 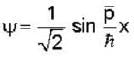
The solution of the differential equation 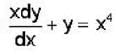 with the boundary condition that y = 1, at x=1 is:—
with the boundary condition that y = 1, at x=1 is:—
A particle of mass 2kg is moving such that at time t second, its position in meter is given by 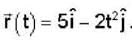 The angular momentum of the particle at t = 2 sec about the origin in kg m2/sec is
The angular momentum of the particle at t = 2 sec about the origin in kg m2/sec is
If z = f(x, y), where x = g(t), y = h(t), g(3) = 2, g'(3) = 5, h(3) = 7, h'(3) = -4, fx(2, 7) = 6, fy(2,7) = -8, then the value of  at t = 3 is
at t = 3 is
If 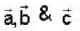 are non coplanar unit vectors such that
are non coplanar unit vectors such that 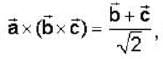 then the angle between
then the angle between  is
is
A system of four particles is in x-y plane of these two particle of masses m are located at (1,1) and (-1,1). The remaining two particles each of mass 2m are located at (1,-1) and (-1,-1). The xy component of moment of inertia tensor of the system of particle is
Consider circular orbits in a central force potential V(r) = 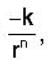 , where k > 0 and o < n < 2. If the time period of a circular orbit of radius R is T1 and that of radius 3R is T3, then
, where k > 0 and o < n < 2. If the time period of a circular orbit of radius R is T1 and that of radius 3R is T3, then 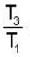 is,
is,
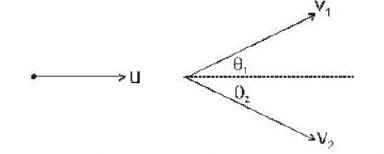
After a perfectly elastic collision of two identical balls, one of which was initially at rest, the velocities of both the balls are non zero. The angle θ between the final.
Velocities (in the lab frame) is
The escape velocity of the earth is v0. For a planet having radius 4 times and density three times that of the earth, the escape velocity will be
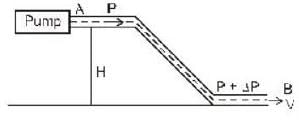
A pump is used to push water of density p through a tube of constant cross- section area ‘A’ shown below. What is the value of ΔP?
Nearest neighbour distance in Na crystal is 1.83 A°. Density of electron in Na crystal is:-
The electric potential due to a linear quadrupole varies inversely with distance ‘r’ as :-
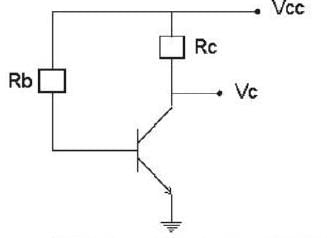
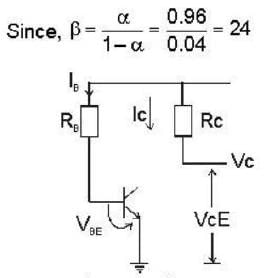
Calculate the collector voltage (Vc) of the transistor circuit shown in the fig be- low :-
Given 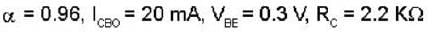
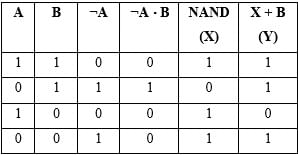
The logic circuit shown in the following figure yields the given truth table.
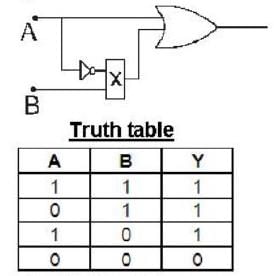
The gate ‘x’ in the diagram is:-
A metal with body centered cubic (bcc) structure shows the first (i.e. smallest angle) diffraction peak at a Bragg angle of θ = 30°. The wavelength of X-ray used is 2.1 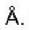 . The volume of the primitive unit cell of the metal is (for first peak, h + k + 1 should be even)
. The volume of the primitive unit cell of the metal is (for first peak, h + k + 1 should be even)
Consider the surface corresponding to the equation 4x2 + y2 + z = 0 .A possible unit tangent to this surface at the point (1,2,-8) is
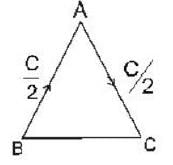
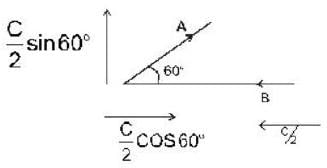
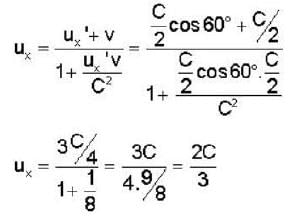
In the laboratory frame, two observers A and B are moving along the sides of an equilateral triangle with equal speeds C/2, as shown in the figure. The speed of B as measured by A will be ______ .
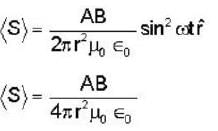
The instantaneous electric and magnetic fields created at a distance r by a point source at the origin are given by

Where ω, A, B are constants and the unit vectors 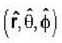 from an orthonormal set. The time averaged power radiated by the source is .
from an orthonormal set. The time averaged power radiated by the source is .
Electric field component of an electromagnetic radiation varies with time as E = 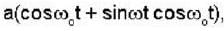 , where a is a constant and the values of the ω and ω0 are 2 x 1015 sec-1 and 1 x 1016 sec-1 respectively. This radiation falls on a metal of work function 4.4eV. The maximum kinetic energy (in eV) of photoelectrons is
, where a is a constant and the values of the ω and ω0 are 2 x 1015 sec-1 and 1 x 1016 sec-1 respectively. This radiation falls on a metal of work function 4.4eV. The maximum kinetic energy (in eV) of photoelectrons is
If E1 is the energy of the electron in the six fold degenerative energy state (1,2,3) in a cubical potential box of side a and E2 is the energy of a particle of mass twice that of electron in the second non-degenerative energy state of a side 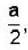 then E2-E1
then E2-E1
Three polarisers P,Q and R are placed parallel to each with their planes perpendicular to the z-axis. Q is placed between P and R Initially, the polarising directions of P and Q are parallel but that of R is perpendicular to them . In this arrangement when unpolarised light of density l0 is incident on P , the R intensity coming out of R is zero, the polariser Q is now rotated about the z-axis. The maximum intensity of light coming out of R is
A diffraction grating having N slits , each of width b and period d , is illuminated normally by a monochromatic plane wave of wavelength λ. What is the phase difference between waves from first and Nth slit in the heighest diffraction order?
The speed of sound propagating in air as a function of temperature T is given by v = αT, where , α is a constant of appropriate dimensions. Calculate the time taken for a sound wave to travel a distance L between two points A and B , If the air temperature between the points varies linearly from T1 to T2.
The extension in a string, obeying Hooke’s law, is x. The speed of transverse wave in the stretched string is V. If the extension in the string is increased to 1.5x, the speed of transverse wave will be
Two radio stations broadcast their programs at the same Amplitude A and at slightly different frequencies ω1 and ω2 respectively, where ω1 - ω2= 103Hz. A detector receives the signals from the two stations simultaneously. It can only detect signals of intensity ≥2A2. Find the time interval between successive maxima of the intensity of the signal received by the detector.
A thin convex lens made from crown glass 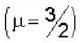 as focal length f. When it is measured in two different liquids having refractive indices
as focal length f. When it is measured in two different liquids having refractive indices 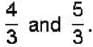 It has the focal length f1 and f2, respectively. The correct relations between the focal length is ________ .
It has the focal length f1 and f2, respectively. The correct relations between the focal length is ________ .
In a YDSE bi-chromatic light of wavelength 400 nm and 560 nm are used. The distance between the slits is 0.1 mm and the distances between the plane of the slits and the screen is 1m. The minimum distance between two successive regions of complete darkness is _______



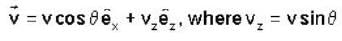
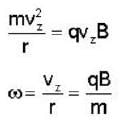
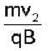
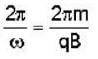
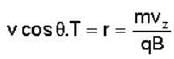
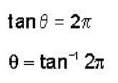
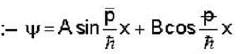
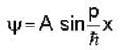
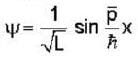

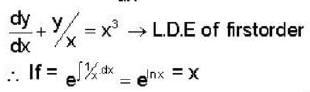
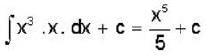
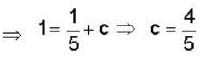

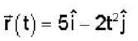


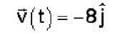
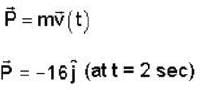

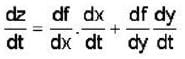
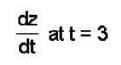
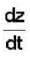 = fx(2, 7).g'(3) + fy(2, 7)h'(3) 6 x 5 + (-8 ) x ( - 4) = 62
= fx(2, 7).g'(3) + fy(2, 7)h'(3) 6 x 5 + (-8 ) x ( - 4) = 62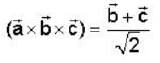
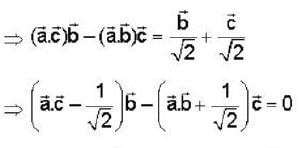
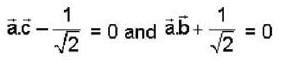
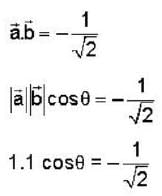
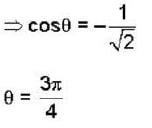
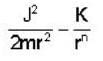
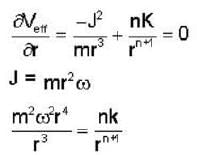
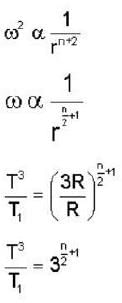
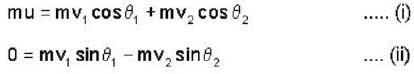
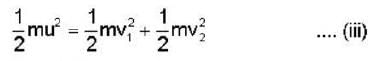

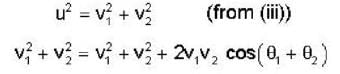
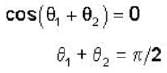


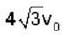
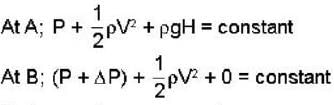
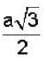
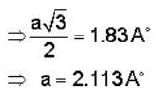
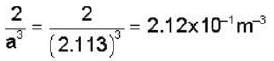

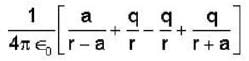
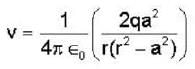
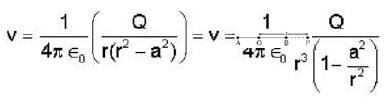
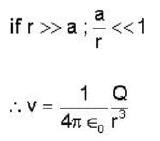
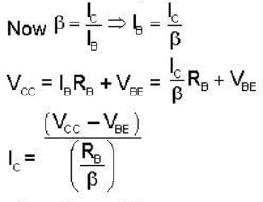
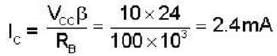
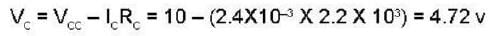
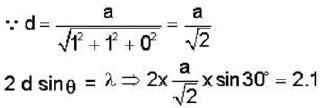
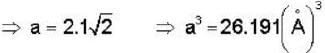
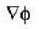
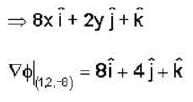

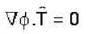
 is tangent
is tangent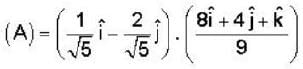
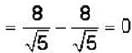
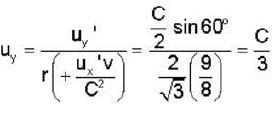
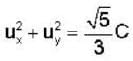

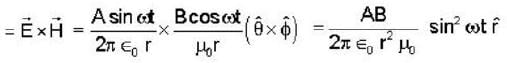
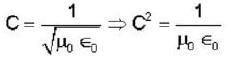
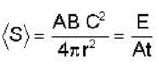



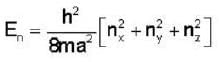
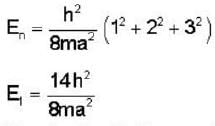
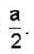
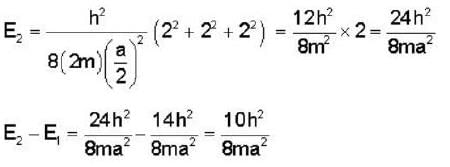
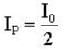
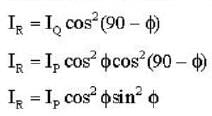
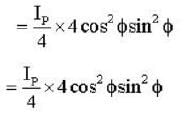
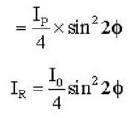
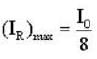
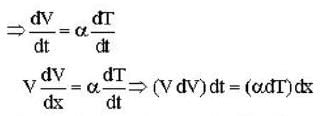
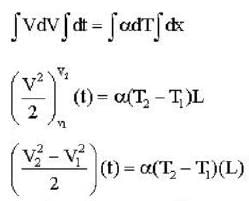
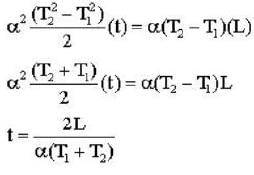
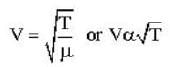
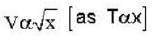
 by times or 1.22 times.
by times or 1.22 times.