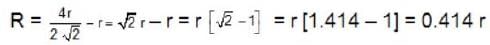GATE Physics Mock Test Series - 6 - Physics MCQ
30 Questions MCQ Test GATE Physics Mock Test Series 2025 - GATE Physics Mock Test Series - 6
The energy density and pressure of aphoton gas are given by 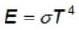 and P =
and P = 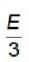 where T is the temperature and σ is the radiation constant. The entropy per unit volume is given by
where T is the temperature and σ is the radiation constant. The entropy per unit volume is given by
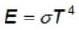 and P =
and P = 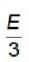 where T is the temperature and σ is the radiation constant. The entropy per unit volume is given by
where T is the temperature and σ is the radiation constant. The entropy per unit volume is given byLet ψ0 and ψ2. denote respectively the ground state and second excited state energy eigenfunction of a particle moving in a harmonic oscillator potential with frequency ψ. If at time t the particle has the wavefunction,
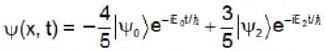
The expectation value of the energy as a function of time
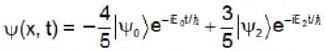
The expectation value of the energy as a function of time
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The wave function of a certain particle is 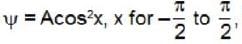 than the value of A is
than the value of A is
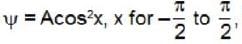 than the value of A is
than the value of A isAt constant temperature on increasing the pressure of a gas by 10% will decrease its volume by
The independent solutions of the equation 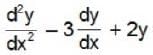 = cos hx are —
= cos hx are —
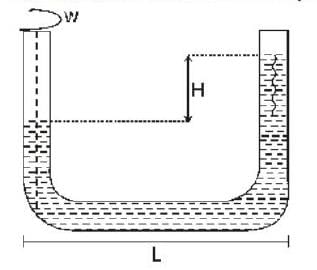
A U-shaped tube contains a liquid of density ρ and it is rotated about the line as shown in the figure. The difference in the levels of liquid column is
The first ball of mass m moving with the velocity v collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
One mole of an ideal monoatomic gas is kept in a volume V and is at temperature T. If the volume and temperature of the gas are respectively changed to V’ and T’ in such a way that the entropy of the gas is unchanged, then which of the following is correct.
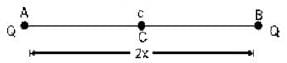
A charge q is placed at the centre of the line joining two equal charges Q. The system of three charges will be in equilibrium if q =
At a given point in space the total light wave is composed of three phases
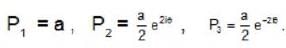
The intensity of light at this point is
A radioactive sample S1 having an activity of 5μCi has twice the number of nuclei as another sample S2 which has an activity of 10μCi. The half lives of S1 and S2 can be
When a plane polarised light is normally incident on half wave plate with an angle 30° to optical axis the output light is
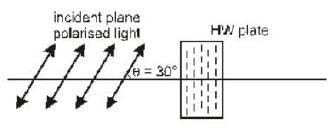
When plane polarized light wave is incident on a quarter wave plate at θ= 45° angle then what is the nature of output wave.
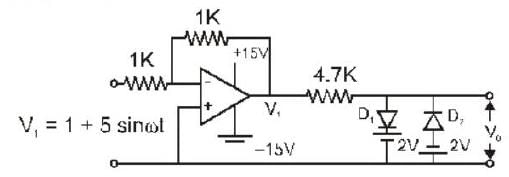
For the circuit shown in the given figure, assuming ideal diodes, the output waveform V0 will be
At normal temperature (0°C) and normal pressure (1.013 x 105 N/m2) when 1 gm. of water freezes, its volume increases by 0.091 cm3. What is the change in internal energy.
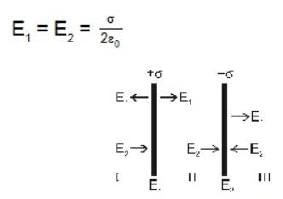
Two infinite parallel plates are uniformly charged. And the charge density on these plates are +σ and - σ respectively. The intensity of electric field between these plates will be
A conductor is placed in a variable electric field  . The ratio of displacement current density to conduction current density is (σ is conductivity)
. The ratio of displacement current density to conduction current density is (σ is conductivity)
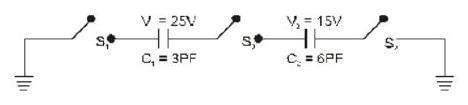
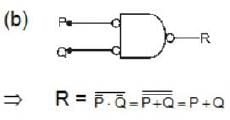
For the circuit shown, which one of the following statement is true?
The internal energy of an ideal gas decreases by the same amount as the work done by the system
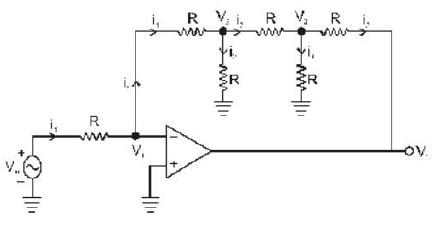
What is the gain V0/Vi of the circuit of figure
In a crystal whose primitives are 1.2A° 1.8A° and 2A°, along whose miller indices are (2, 3, 1) cuts intercept 1.2 A° along X - axis. What will be the length of intercepts along y and z - axes.
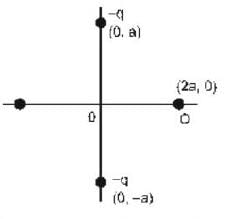
Two equal negative charges -q are fixed at points (0, -a) and (0, a) on y-axis. A positive charge Q is released from rest at the point (2a, 0) on the x-axis. The charge Q will be
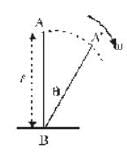
A uniform rod of length I is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest from its unstable equilibrium position . When it has turned through an angle θ , its angular velocity ω is given as
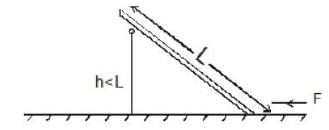
Consider the situation shown in the figure. All the surfaces are smooth and the rod has mass M what is the minimum value of F required to keep the rod in equilibrium ?
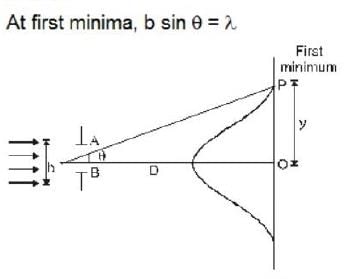
A parallel monochromatic beam of light is incident normally on a narrow slit. A diffraction pattern is formed on a screen placed perpendicular to the direction of the incident beam. At the first minimum of the diffraction pattern, the phase difference between the rays coming from the two edges of the slit is
In a p-n junction diode not connected to any circuit
A planet of mass m and angular momentum L moves in a circular orbit in a potential v(r)= 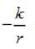 where k is a positive constant If the planet is slighthy perturbed, find angular frequency of radial oscillation.
where k is a positive constant If the planet is slighthy perturbed, find angular frequency of radial oscillation.
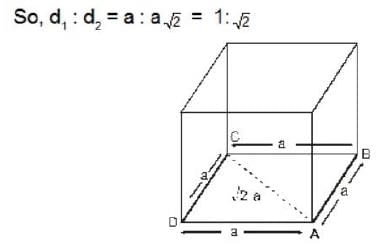
What is the ratio of the nearest neighbour distance to the next nearest neighbour distance in a simple cubic crystal
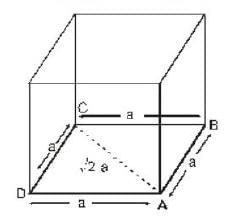
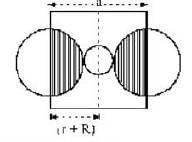
What is the maximum radius of the sphere that can just fit into the void at the body centre of the fee structure coordinated by the facial atom. Given r is the radius of atom.
|
1 docs|34 tests
|


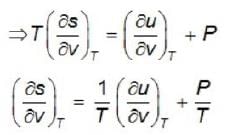
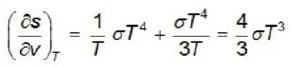
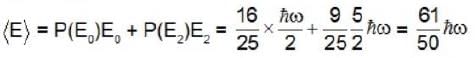
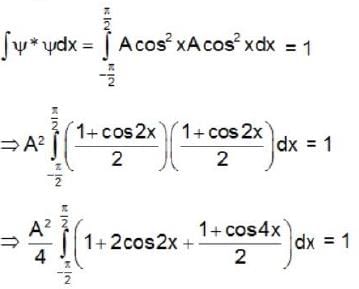
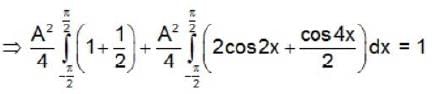
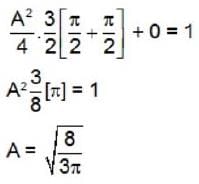


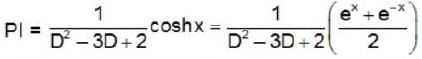
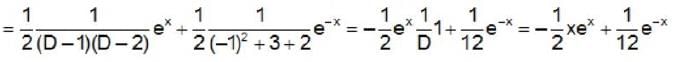
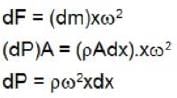
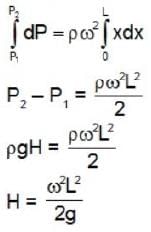
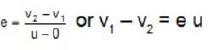 ....(ii)
....(ii)
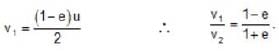

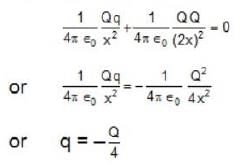
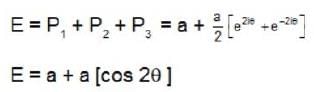
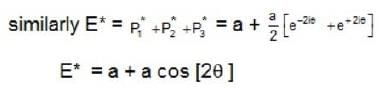
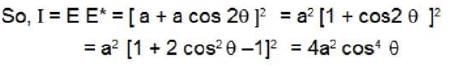
 (Activity of S2)
(Activity of S2)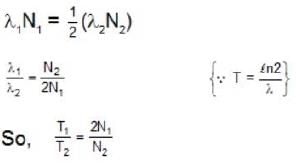
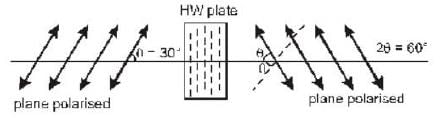
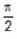 and path difference is
and path difference is 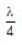 so, output light is circularly polarised
so, output light is circularly polarised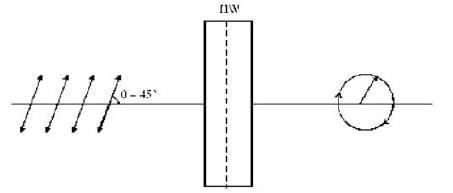


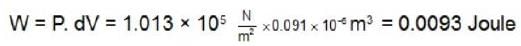

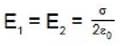
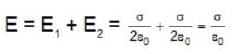
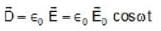

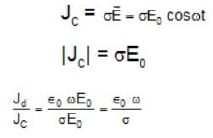
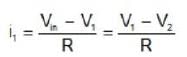
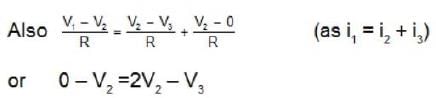
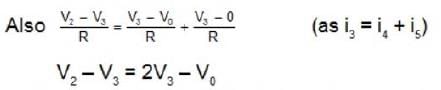
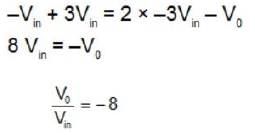

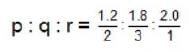
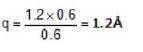
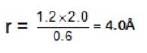

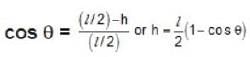
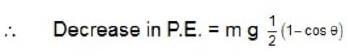 ..(1)
..(1)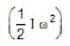
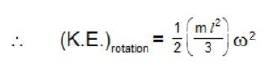 ..(2)
..(2)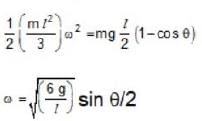
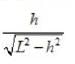
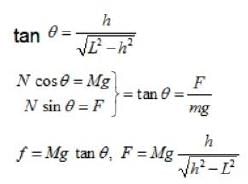
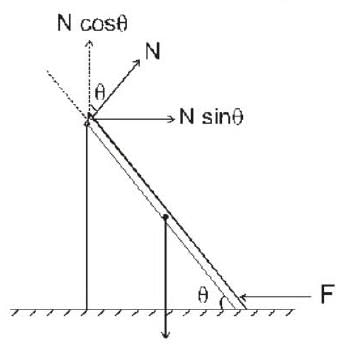

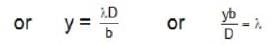 ...(1)
...(1)
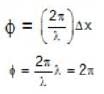
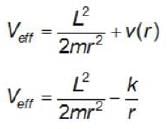
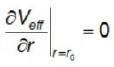

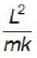 Angular frequency of oscillation
Angular frequency of oscillation