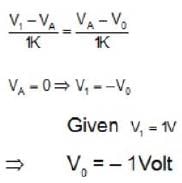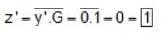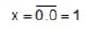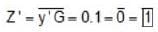GATE Physics Mock Test Series - 7 - Physics MCQ
30 Questions MCQ Test GATE Physics Mock Test Series 2025 - GATE Physics Mock Test Series - 7
If an integral curve of the differential equation 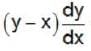 = 1 passes (0.0) and (α,1), then α is equal to
= 1 passes (0.0) and (α,1), then α is equal to
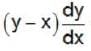 = 1 passes (0.0) and (α,1), then α is equal to
= 1 passes (0.0) and (α,1), then α is equal toThe potential φ in Joule of a particle of mass 1 kg moving in x - y plane obey the law of φ = 3x + 4y. Here x and y are in meters. If the particle is at rest at (6m, 8m) at time t = 0, then the work done by conservative force on the particle from the initial position to the instant when it crosses the x - axis is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A solid uniform disc of mass m rolls without slipping down a fixed inclined plank with an acceleration α. The frictional force on the disc due to surface of the plane is
Consider the earth as a uniform sphere of mass M and radius R. Imagine a straight smooth tunnel made through the earth which connects any two points on its surface. The motion of a particle of mass m along this tunnel under the action of gravitation simple harmonic. Determine the time that a particle would take to go from one end to the other through the tunnel.
A glass plate of thickness 30 mm is placed just below a well-focused microscope for focusing it again the microscope should be moved through a distance of :
The Clausius-clapeyron equation indicates that the increase of pressure increases the melting point.
The magnitude of the de-Broglie wavelength λ of electron (e), proton (p), neutron (n) and α - particle (α) all having the some energy of 1 MeV, in the increasing order will follow which of the following sequence :
The frequency of a cyclotron oscillator is 107 Hz. The cyclotron is accelerating protons. If the radius of the does of the cyclotron be 0.6 m, the kinetic energy of the proton beam produced by the accelerator will be nearly_______ .
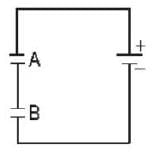
Two identical capacitors A and B shown in the given circuit are joined in series with a battery. If a dielectric slab of dielectric constant K is slipped between the plates of capacitor B and battery remain connected then the energy of capacitor A will
Consider a particle with three possible spin state S = 0 and ±1. There is a magnetic field h present and the energy for a spin state S is -hS. The system is at a temperature T. Which of the following statements is true about the entropy S(T) ?
Consider three situations of 6 particles in one dimensional box of width L with hard walls. In case (i), the particles are fermions, in case (ii) they are bosons and in case (iii) they are classical. If the total ground state energy of the six particles in these three cases are EF, EB and Ecl respectively, which of the following is correct ?
The electric fields inside (r < R) and outside (r > R) a solid sphere with a uniform volume charge density are given by 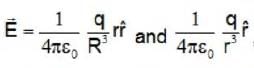 , respectively, while the electric field outside a spherical shell with a uniform surface charge density is given by
, respectively, while the electric field outside a spherical shell with a uniform surface charge density is given by 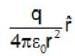 being the total charge. The correct ratio of the electrostatic energies for the first case to second case is
being the total charge. The correct ratio of the electrostatic energies for the first case to second case is
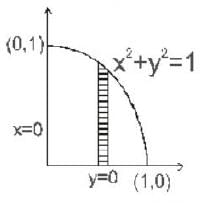
Le t 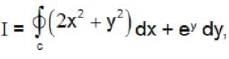 where c is the boundary (oriented anticlockwise ) of the region in the first quadrant bounded by y = 0, x2 + y2 = 1 and x = 0. The value of I is
where c is the boundary (oriented anticlockwise ) of the region in the first quadrant bounded by y = 0, x2 + y2 = 1 and x = 0. The value of I is
A quantum mechanical particle in a harmonic oscillator potential has the initial wave function 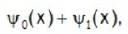 , where ψ0 and ψ1 are the real wave functions in the ground and first excited state of the harmonic oscillator. For convenience we take m = ℏ = ψ= 1 for the oscillator. What is the probability density of finding the particle at x at time t = π ?
, where ψ0 and ψ1 are the real wave functions in the ground and first excited state of the harmonic oscillator. For convenience we take m = ℏ = ψ= 1 for the oscillator. What is the probability density of finding the particle at x at time t = π ?
A particle of mass m is thrown upward with velocity v and there is retarding air resistance proportional to the square of the velocity with proportionality constant K. If the particle attains a maximum height after time t, and g is the gravitational acceleration, what is the velocity.
A monochromatic wave propagating in a direction making an angle 30° with the y-axis in the reference frame of source. The source moves at speed v  towards the observer. The direction of the (cosine of angle) wave as seen by the observer’s _____ .
towards the observer. The direction of the (cosine of angle) wave as seen by the observer’s _____ .
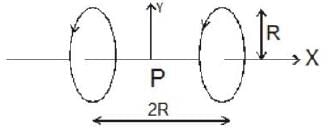
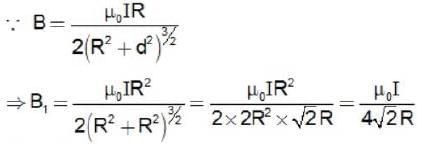
A system of two circular co-axial coils carrying equal currents i along same direction having equal radius R and separated by a distance 2R (as shown in figure below). The magnitude of magnetic field at the midpoint P is given by
Consider a system of 4N non-interacting spin 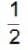 particles each fixed in position and carrying a magnetic moment μ . The system is immersed in a uniform magnetic field B. The number of spin down particle for which the entropy of the system will be maximum is
particles each fixed in position and carrying a magnetic moment μ . The system is immersed in a uniform magnetic field B. The number of spin down particle for which the entropy of the system will be maximum is
The spectral emission power of a black body at 6000K is maximum at 5000˙A . If the temperature is increased by 10% then decrease in the value λm will be
Let 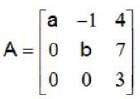 be a matrix with real entries. If the sum and the product of all the eigen values of A are 10 and 30, respectively, then a2+b2 equals
be a matrix with real entries. If the sum and the product of all the eigen values of A are 10 and 30, respectively, then a2+b2 equals
A 150Ω resister, a l0μf capacitor a 0.1 H inductor are connected in series to an AC source operating at an angular frequency ω, for what ω the combination acts as a pure resistive load.
Consider two electromagnetic plane waves propagating in vacuum with their electric field vectors
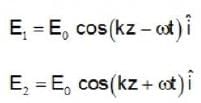
then the averaged pointing vector for the resultant wave
A convex lens of focal length 24 cm (μ = 1.5) is totally immersed in water. Its focal length in water is _______ .
Unpoiarized light falls on two polarizing sheets placed on top of the other. What be the angle between the characteristic directions of the sheets if the intensity of the transmitted light is one third intensity of the incident beam_______ .
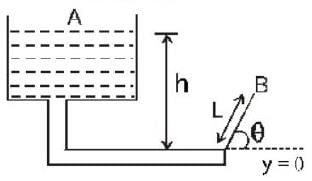
What is the maximum range along the dashed line attained by the water stream coming out at B from a thin tube of the water tank assembly shown in the figure ?
Assume h = 10m, L = 2m and θ = 30°
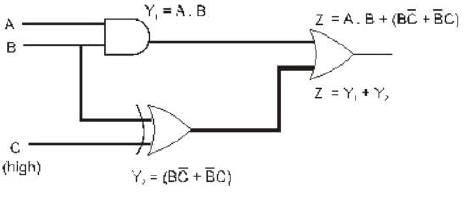
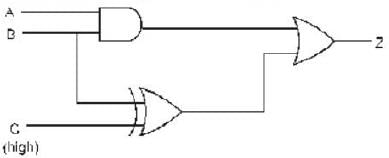
Consider the digital circuit shown below in which the input C is always high (1)
The truth table for the circuit can be written as
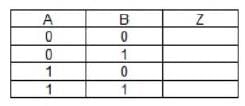
The entries in the Z column (vertically) are
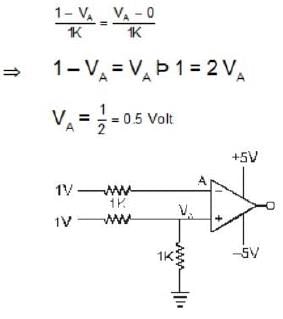
In the operational amplifier circuit below, the voltage at point A is
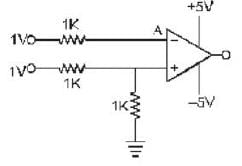
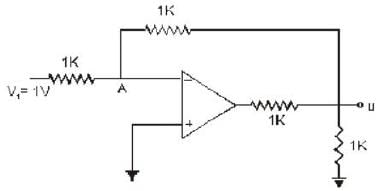
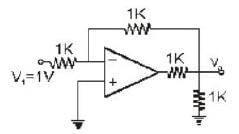
In the op-amp circuit shown in the figure below, the input voltage V1 is 1V. The value of the output Vo is
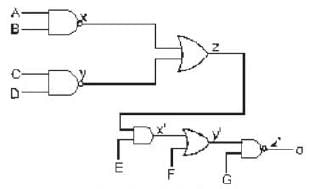
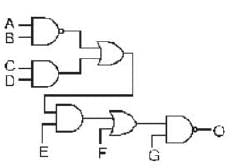
The output, 0, of the given circuit is cases I and II, where
Case I : A, B = 1; C, D = 0; E, F = 1 and G = 0
Case II : A, B = 0; C, D = 0; E, F = 0 and G = 1
are, respectively
|
1 docs|34 tests
|


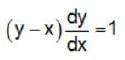
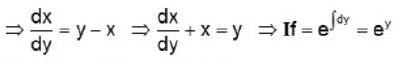
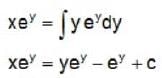
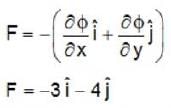
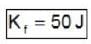
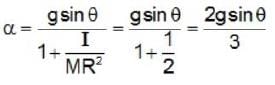


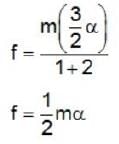
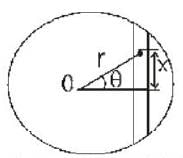
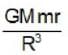

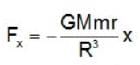

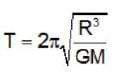
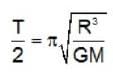
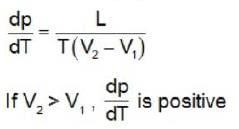
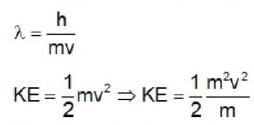
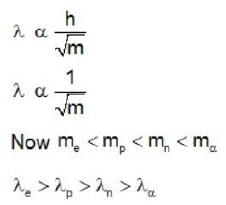
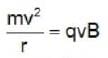
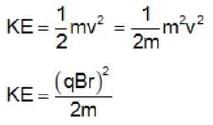
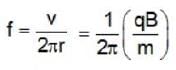
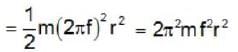
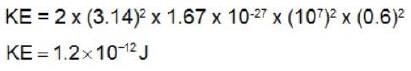
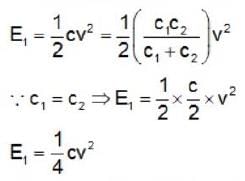

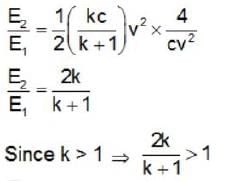
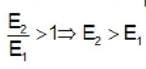 ∵ energy increases.
∵ energy increases.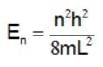
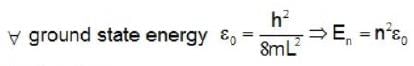
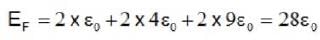
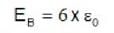
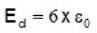

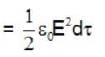
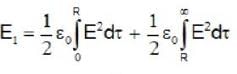
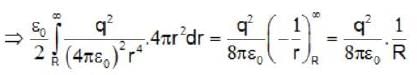
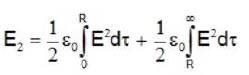
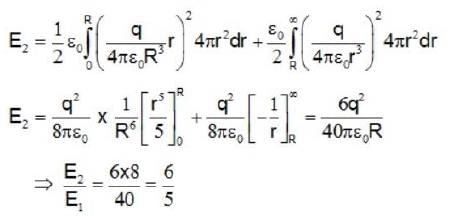
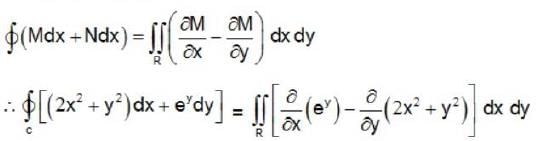
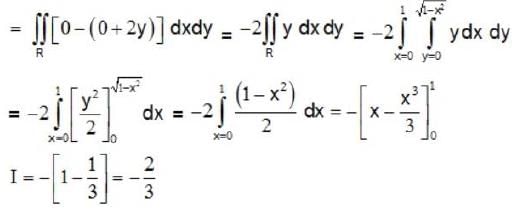
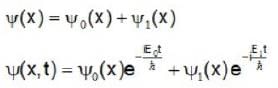
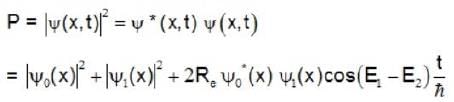
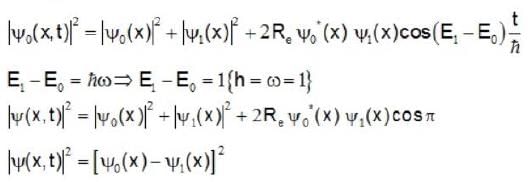
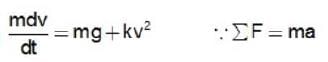
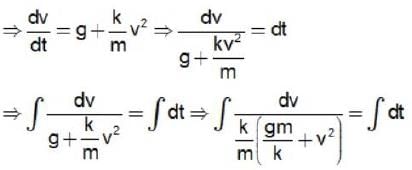
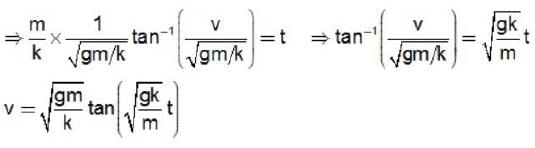
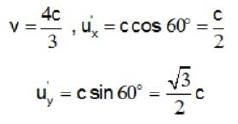
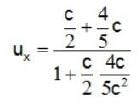
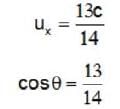
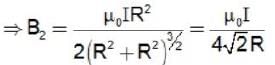
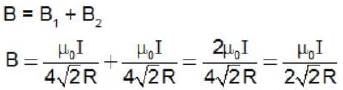
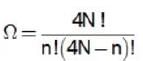
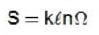
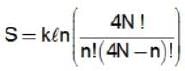
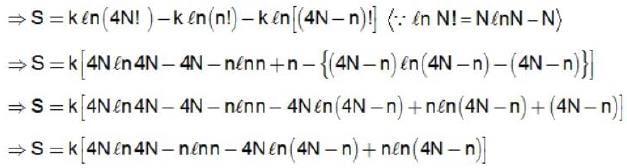
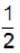 down particle
down particle 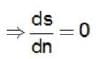
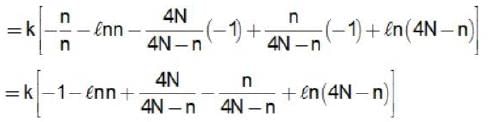

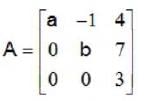
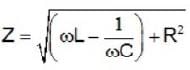
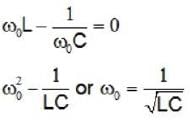
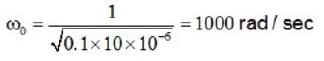
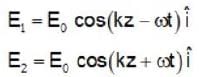
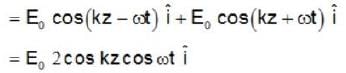
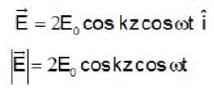

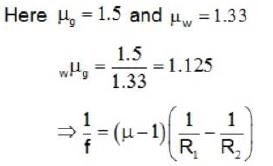
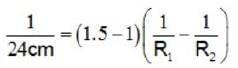
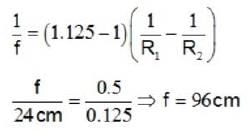
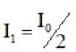
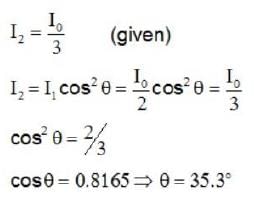
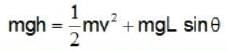
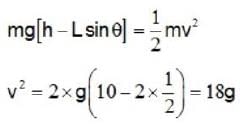
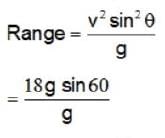
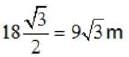
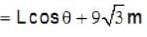
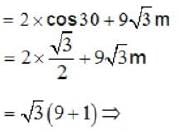
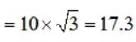
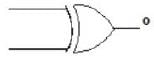 This is X-OR-GATE in which when both inputs are same
This is X-OR-GATE in which when both inputs are same 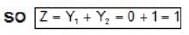 ... (a)
... (a)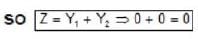 ... (b)
... (b) .... (c)
.... (c)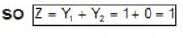 .....(d)
.....(d)