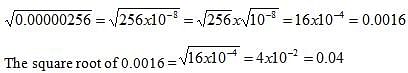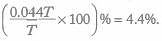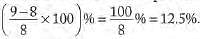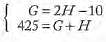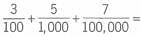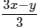GMAT Classic Mock Test - 10 - GMAT MCQ
30 Questions MCQ Test Mock Test series for GMAT Classic Edition - GMAT Classic Mock Test - 10
Directions: Solve the problem and select the best of the answer choices given.
Q. What is the value of the square root of the square root of .00000256?
Directions: Solve the problem and select the best of the answer choices given.
Q. Which of the following is NOT a possible value of 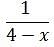
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions: Solve the problem and select the best of the answer choices given.
Q. Which of the following numbers has the greatest number of unique digits?
Directions: Solve the problem and select the best of the answer choices given.
Q. What is the value of y less than x?
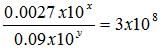
Directions: Solve the problem and select the best of the answer choices given.
Q. If x and y are positive integers, what percent of three more than y is twice the value of x?
Of the total amount that Jill spent on a shopping trip, excluding taxes, she spent 50 percent on clothing, 20 percent on food, and 30 percent on other items. If Jill paid a 4 percent tax on the clothing, no tax on the food, and an 8 percent tax on all other items, then the total tax that she paid was what percent of the total amount that she spent, excluding taxes?
How many integers x satisfy both 2 < x ≤ 4 and 0 ≤ x ≤ 3 ?
At the opening of a trading day at a certain stock exchange, the price per share of stock K was $8. tf the price per share of stock K was $9 at the closing of the day, what was the percent increase in the price per share of stock K for that day?
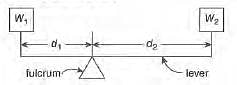
As shown in the diagram below, a lever resting on a fulcrum has weights of w1 pounds and w2 pounds, located d1 feet and d2 feet from the fulcrum. The lever is balanced and w1d1 = w2d2. Suppose w1 is 50 pounds and w2 is 30 pounds, fIf d1 is 4 feet less than d2 what is d2, in feet?
The number of rooms at Hotel G is 10 less than twice the number of rooms at Hotel H. If the total number of rooms at Hotel G and Hotel H is 425, what is the number of rooms at Hotel G?
If r and s are positive integers such that (2r)(4s) = 16, then 2r + s =
Three people each contributed x dollars toward the purchase of a car. They then bought the car for y dollars, an amount less than the total number of dollars contributed. If the excess amount is to be refunded to the three people in equal amounts, each person should receive a refund of how many dollars?
In the system of equations below, what is the value of X?
2x + 2y = -4
4x + y = 1
At Rounders Grocer, orange slices cost $2 a pound, pineapple chunks cost $3 a pound, and cut watermelon cost $5 a pound. If Sally buys enough of these three fruits from Rounders to make five pounds of fruit salad, and at least one pound of each, which fruit did she buy the most of by weight?
(1) Sally spent less than $5 on orange slices.
(2) Sally spent more than $18 on her fruit salad.
In ΔXYZ, what is the length of YZ?
(1) The length of XY is 3.
(2) The length of XZ is 5.
A supermarket display of canned corn is shaped like a pyramid with one can on top and two more cans in each row below. If the display is only one can deep for the entire pyramid, what is the median number of cans in a row in the pyramid?
(1) There are 100 cans in the pyramid.
(2) The range of cans per row is 18.
K is a set of numbers such that
(i) if x is in K, then -x is in K, and
(ii) if each of x and y is in K, then xy is in K
Is 12 in K?
(1) 2 is in K.
(2) 3 is in K,
Define two sets as follows:
A= {2, 4, 6, 8, 10, a, b}
B = {1, 3, 5, 7, 9, c, d}
where a and b are distinct positive odd integers and c and d are distinct positive even integers.
How many elements are contained in the set A ∩ B ?
1) a,b ∈ {1, 3, 5, 7, 9}
2) c,d ∈ {2, 4, 6, 8, 10}
After winning 50 percent of the first 20 games it played, Team A won all of the remaining games it played. What was the total number of games that Team A won?
(1) Team A played 25 games altogether.
(2) Team A won 60 percent of all the games it played.
How many elements are in the set ?
Statement 1: has three more elements than .
Statement 2: includes exactly four elements not in .
If m and n are nonzero integers, is mn an integer?
(1) nm is positive.
(2) nm is an integer.
A = {2,4,6,8,10,12,...}
B = {3,6,9,12,15,18...}
True or false: n∈A∪B
Statement 1: n is a perfect square.
Statement 2: n is a multiple of 99.
If n is the least of three different integers greater than 1, what is the value of n ?
(1) The product of the three integers is 90.
(2) One of the integers is twice one of the other two integers.
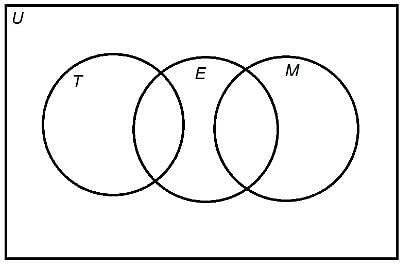
In the below Venn diagram, universal set U represents the residents of Jonesville. The sets T,E,M represent the set of all Toastmasters, Elks, and Masons, respectively.
Jerry is a resident of Jonesville. Is he a Mason?
Statement 1: Jerry is a Toastmaster.
Statement 2: Jerry is not an Elk.
Michael arranged all his books in a bookcase with 10 books on each shelf and no books left over. After Michael acquired 10 additional books, he arranged all his books in a new bookcase with 12 books on each shelf and no books left over. How many books did Michael have before he acquired the 10 additional books?
(1) Before Michael acquired the 10 additional books, he had fewer than 96 books.
(2) Before Michael acquired the 10 additional books, he had more than 24 books.
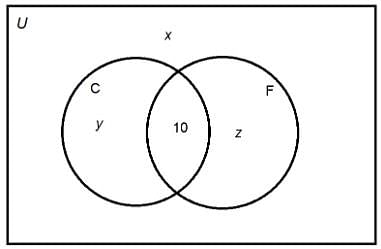
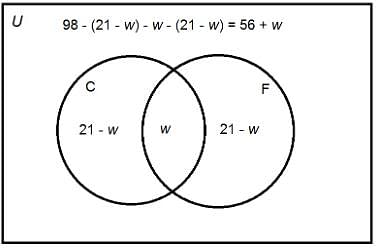
Two of the courses from which the 98 freshmen at a high school may choose are French and Creative Writing.
How many freshmen enrolled in neither course?
Statement 1: 10 freshmen enrolled in both courses.
Statement 2: 21 freshmen enrolled in each course.
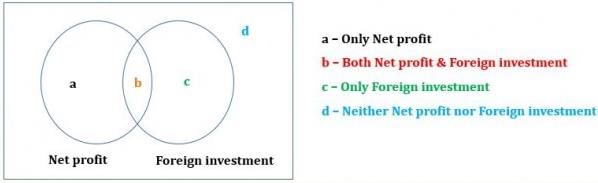
Last year in a group of 30 businesses, 21 reported a net profit and 15 had investments in foreign markets. How many of the businesses did not report a net profit nor invest in foreign markets last year?
(1) Last year 12 of the 30 businesses reported a net profit and had investments in foreign markets.
(2) Last year 24 of the 30 businesses reported a net profit or invested in foreign markets, or both.
Two hydrochloric acid solutions, one of concentration 40% and one of concentration 25%, are mixed together to make a solution of 35% concentration.
How much solution is made?
(1) 200 ml of 40% solution is used
(2) 100 ml of 25% solution is used
|
39 docs|15 tests
|
|
39 docs|15 tests
|