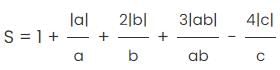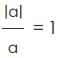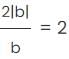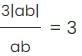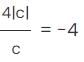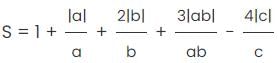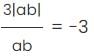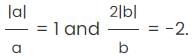GMAT Classic Mock Test - 7 - GMAT MCQ
30 Questions MCQ Test - GMAT Classic Mock Test - 7
Computer Games Plus needs to get rid of its copies of an old computer game. If it lowers the cost of the old computer game by $5 dollars, it can increase sales of the old computer game by 10 units and still generate exactly $100 of revenue from the old game. How many units of the old computer game did Computer Games Plus sell after implementing the new selling strategy?
x, y, and z are consecutive positive integers such that x < y < z; which of the following must be true?
1. xyz is divisible by 6
2. (z-x)(y-x+1)=4
3. xy is odd
1. xyz is divisible by 6
2. (z-x)(y-x+1)=4
3. xy is odd
At a local appliance manufacturing facility, the workers received a 20% hourly pay raise due to extraordinary performance. If one worker decided to reduce the number of hours that he worked so that his overall pay would remain unchanged, by approximately what percent would he reduce the number of hours that he worked?
z is a positive integer and multiple of 2; p = 4z, what is the remainder when p is divided by 10?
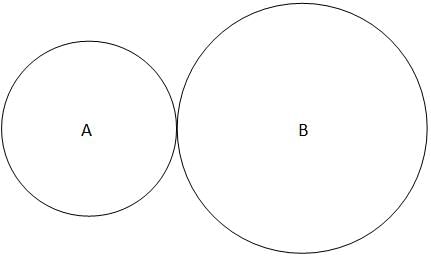
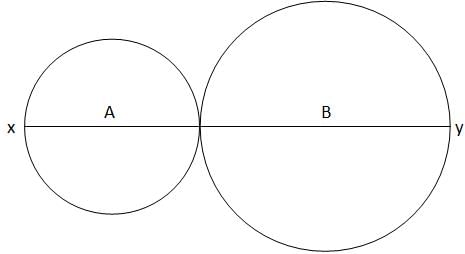
In the above figure, the area of circle A is 144π and the area of circle B is 169π. If point x (not shown above) lies on circle A and point y (not shown above) lies on circle B, what is the range of the possible lengths of line xy.
Set S consists of the following unique integers: -2, 17, 3, n, 2, 15, -3, and -27; which of the following could be the median of set S?
There are six different models that are to appear in a fashion show. Two are from Europe, two are from South America, and two are from North America. If all the models from the same continent are to stand next to each other, how many ways can the fashion show organizer arrange the models?
A group of seven students is to be seated in a row of seven desks. In how many different ways can the group be seated if two of the preselected students must sit in an end seat (i.e., two students have been preselected to sit in either the first or the seventh seat)?
If x is a positive integer such that (x - 1)(x - 3)(x - 5)....(x - 93) < 0, how many values can x take?
If two distinct integers a and b are picked from {1, 2, 3, 4, .... 100} and multiplied, what is the probability that the resulting number has EXACTLY 3 factors ?
Working alone at their respective constant rates, A can complete a task in ‘a’ days and B in ‘b’ days. They take turns in doing the task with each working 2 days at a time. If A starts they finish the task in exactly 10 days. If B starts, they take half a day more. How long does it take to complete the task if they both work together?
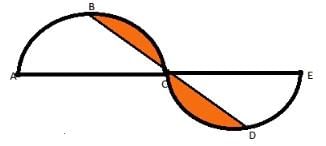
In the figure given below, ABC and CDE are two identical semi-circles of radius 2 units. B and D are the mid points of the arc ABC and CDE respectively. What is the area of the shaded region?
If a, b, and c are not equal to zero, what is the difference between the maximum and minimum value of S? S = 1 + 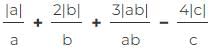
Consider a set S = {2, 4, 6, 8, x, y} with distinct elements. If x and y are both prime numbers and 0 < x < 40 and 0 < y < 40, which of the following MUST be true?
I. The maximum possible range of the set is greater than 33.
II. The median can never be an even number.
III. If y = 37, the average of the set will be greater than the median.
If x and y are integers and |x - y| = 12, what is the minimum possible value of xy?
How many members of the staff of Advanced Computer Technology Consulting are women from outside the United States?
1. one-fourth of the staff at Advanced Computer Technology Consulting are men
2. 20% of the staff, or 20 individuals, are men from the U.S.; there are twice as many women from the U.S. as men from the U.S.
If x and y are integers, what is the ratio of 2x to y?
1. 8x3 = 27y3
2. 4x2 = 9y2
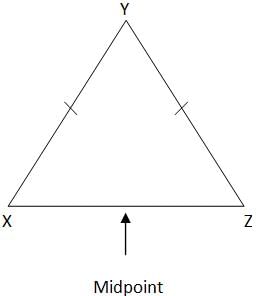
X, Y, and Z are three points in space; is Y the midpoint of XZ?
1. ZY and YX have the same length
2. XZ is the diameter of a circle with center Y
15a + 6b = 30, what is the value of a-b?
1. b = 5 – 2.5a
2. 9b = 9a – 81
What is the value of (n + 1)2?
n2 - 6n = -9
(n-1)2 = n2 – 5
John’s Pack and Ship uses price discrimination to capture consumer surplus. How much revenue did John's firm earn last week if it shipped 100 packages for customers?
1. For 75% of the packages John shipped, he charged the store-front rate. John charged the bulk-rate for the remainder of the packages.
2. John’s store-front rate was $4, more than double his bulk-rate.
What is the remainder of a positive integer N when it is divided by 2?
1. N contains odd numbers as factors
2. N is a multiple of 15
If m and n are non-zero integers, is mn > nn?
Statement 1: |m| = n
Statement 2: m < n
What is the remainder when the positive integer x is divided by 6?
Statement 1: When x is divided by 7, the remainder is 5.
Statement 2: When x is divided by 9, the remainder is 3.
A candy manufacturer decided to decrease the weight of each candy bar, while retaining the price. By how many cents did the per kilogram cost of candy change after the reduction in weight?
Statement 1: The weight of each piece of candy bar reduced by 9 grams.
Statement 2: The weight of each piece of candy bar reduced by 9%
a, b, and c are sides of a right triangle. What is the area of the triangle?
Statement 1: a = 4.
Statement 2: a + b + c = 4.
GMAT Challenging Math Question | Arithmetic | Number Properties DS Practice
Is |x| > x?
Statement 1: x2 + y2 = 4
Statement 2: x3 + y2 = 0
Is the triangle ABC right angled at B an isosceles triangle?
Statement 1: All 3 sides are integers.
Statement 2: The square of the hypotenuse is twice the product of the other two sides.
x is a two-digit positive integer. y is obtained by multiplying the tens place of x by 2. Is y > x/6?
Statement 1: 20 < x < 30
Statement 2: y = 10
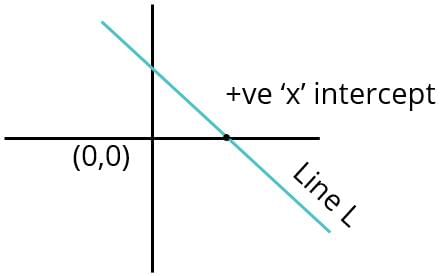
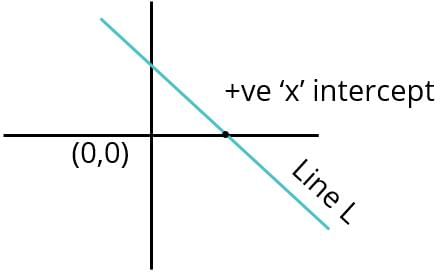
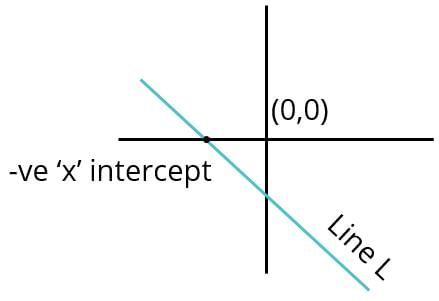
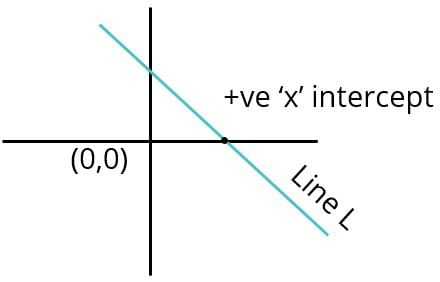
Does the line L whose equation is y = mx + c cut the x-axis in the positive direction of x-axis?
Statement 1: The intercepts of Line K, perpendicular to L, are of the opposite signs.
Statement 2: Line L passes through the 4th quadrant.




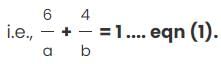
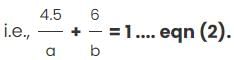

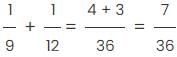 th of the task in a day.
th of the task in a day.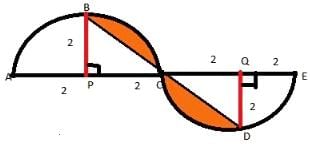
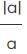 = 1 When a is positive.
= 1 When a is positive.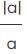 = 1 When a is negative.
= 1 When a is negative.