Gaseous State MCQ- 1 (Advanced) - JEE MCQ
20 Questions MCQ Test - Gaseous State MCQ- 1 (Advanced)
Following graph is constructed for the fixed amount of the gas.
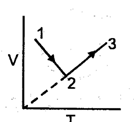
Incorrect statements are :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the pressure of the gas contained in a closed vessel is increased by 20% when heated by 273°C then it's initial temperature must have been.
A mixture of H2 and O2 in 2:1 volume is allowed to diffuse through a porous partition what is the composition of gas coming out initially
There are three closed containers in which equal amount of the gas are filled.If the containers are placed at the same temperatures then find the correct options:
If the rms velocity of nitrogen and oxygen molecule are same at two different temperature and same pressure then.
X ml of H2 gas effuses through a hole in a container in 5 secs. The time taken for effusion of same volume of gas specified below under identical condition is
With reference to the above graph, choose the correct alternatives
The system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at T.K. standard vapour pressure of A and B are PA° and PB° respectively at TK. We collect the vapour of A and B in two container of volume V, first container is maintained at 2TK and second container is maintained at 3T
K.
2
At the
temperature greater than TK, both A and B exist in only gaseous form. Total vapour pressure of the system at TK is given as PT = PA°XA+ PB°XB
Where XA and XB are the mole fraction of A and B in liquid a mixture.
In container (1) We assume that collected gases behave ideally at 2TK and there can take place isomerisation reaction in which A converted into B by first order kinetics Reaction is given as
In Container (II) At the given temperature 3T/2
, A and B are ideal in nature and non mixing in nature. A small pin hole is made container. We can determine the initial rate of effusion of both gases in vacuum by the expression
Where P = pressure difference between system and surrounding K = positive constant M = Molecular weight of the gas.
Q.
If partial vapour pressure of A is twice that of partial vapour pressure of B and total V.P. is equal to 2T at T = 50 K and V = B.21 lit, then number of mole of A and B in vapour phase is :
The system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at T.K. standard vapour pressure of A and B are PA° and PB° respectively at TK. We collect the vapour of A and B in two container of volume V, first container is maintained at 2TK and second container is maintained at 3T
K.
2
At the
temperature greater than TK, both A and B exist in only gaseous form. Total vapour pressure of the system at TK is given as PT = PA°XA+ PB°XB
Where XA and XB are the mole fraction of A and B in liquid a mixture.
In container (1) We assume that collected gases behave ideally at 2TK and there can take place isomerisation reaction in which A converted into B by first order kinetics Reaction is given as
In Container (II) At the given temperature 3T/2
, A and B are ideal in nature and non mixing in nature. A small pin hole is made container. We can determine the initial rate of effusion of both gases in vacuum by the expression
Where P = pressure difference between system and surrounding K = positive constant M = Molecular weight of the gas.
Q.
Vapour is collected and passed into a container of volume 8.21 lit, maintainer at 50 K and after 5 min number of mole of B = 8/3. Then calculate pressure develop into the container after two half lives.
The system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at T.K. standard vapour pressure of A and B are PA° and PB° respectively at TK. We collect the vapour of A and B in two container of volume V, first container is maintained at 2TK and second container is maintained at 3T
K.
2
At the
temperature greater than TK, both A and B exist in only gaseous form. Total vapour pressure of the system at TK is given as PT = PA°XA+ PB°XB
Where XA and XB are the mole fraction of A and B in liquid a mixture.
In container (1) We assume that collected gases behave ideally at 2TK and there can take place isomerisation reaction in which A converted into B by first order kinetics Reaction is given as
In Container (II) At the given temperature 3T/2
, A and B are ideal in nature and non mixing in nature. A small pin hole is made container. We can determine the initial rate of effusion of both gases in vacuum by the expression
Where P = pressure difference between system and surrounding K = positive constant M = Molecular weight of the gas.
Q.
If vapour is collected in container of volume 8.21 lit maintained at 75 K then ratio of initial rate of effusion of Gas A and B is given as:
Gas 'A' (Molar Mass of A= 128 g mol-1) is taken in a closed container at the initial total pressure of 1000 mm of Hg. Pressure of the gas decreases to 900 torr in 5 seconds due to the diffusion though square cross section. Another similar size container is taken in which gaseous mixture of A and B are taken. (Molar mass of the mix is 472/5)
at the total pressure of 5000 torr (molar mass of B = 72 g moll. A rectangular crosssection is made in this container and gases are allowed to duffuse. Width of this rectangular cross-section is same as the side of the square cross section and length of the rectangular cross-section is 50% more than the width. Assume that the gases A and B are non reacting and rate of diffusion of the gases are only dependent upon the initial total pressure and it is independent of the change in the pressure due to diffusion. Assume all other conditions to be identical.
Q.
Gas diffused out initially from 2nd container has composition:
Gas 'A' (Molar Mass of A= 128 g mol-1) is taken in a closed container at the initial total pressure of 1000 mm of Hg. Pressure of the gas decreases to 900 torr in 5 seconds due to the diffusion though square cross section. Another similar size container is taken in which gaseous mixture of A and B are taken. (Molar mass of the mix is 472/5)
at the total pressure of 5000 torr (molar mass of B = 72 g moll. A rectangular crosssection is made in this container and gases are allowed to duffuse. Width of this rectangular cross-section is same as the side of the square cross section and length of the rectangular cross-section is 50% more than the width. Assume that the gases A and B are non reacting and rate of diffusion of the gases are only dependent upon the initial total pressure and it is independent of the change in the pressure due to diffusion. Assume all other conditions to be identical.
Q.
Ratio of the number of moles of A and B left in the container after 10 seconds from the diffusion starts is:
Gas 'A' (Molar Mass of A= 128 g mol-1) is taken in a closed container at the initial total pressure of 1000 mm of Hg. Pressure of the gas decreases to 900 torr in 5 seconds due to the diffusion though square cross section. Another similar size container is taken in which gaseous mixture of A and B are taken. (Molar mass of the mix is 472/5)
at the total pressure of 5000 torr (molar mass of B = 72 g moll. A rectangular crosssection is made in this container and gases are allowed to duffuse. Width of this rectangular cross-section is same as the side of the square cross section and length of the rectangular cross-section is 50% more than the width. Assume that the gases A and B are non reacting and rate of diffusion of the gases are only dependent upon the initial total pressure and it is independent of the change in the pressure due to diffusion. Assume all other conditions to be identical.
Q.
What is the time after which container will have same number of moles of A and B:
When a sample of ideal gas is changed from an initial state to a final state, various curves can be plotted for the process like P - V curve, V - T curve, P - T curve etc.
For example, P - V curve for a fixed amount of an ideal gas at constant temperature is a rectangular hyperbola, V - T curve for a fixed amount of an ideal gas at constant pressure is a straight line and P - T curve for a fixed amount of an ideal gas at constant volume is again a straight line. However, the shapes may vary if the constant parameters are also changed.
Now, answer the following questions:
Q.
Which of the following statements is correct regarding a fixed amount of ideal gas undergoing the following process:
.
= Constant ∵ P2V = Constant or PV1/2 = ConstantWhen a sample of ideal gas is changed from an initial state to a final state, various curves can be plotted for the process like P - V curve, V - T curve, P - T curve etc.
For example, P - V curve for a fixed amount of an ideal gas at constant temperature is a rectangular hyperbola, V - T curve for a fixed amount of an ideal gas at constant pressure is a straight line and P - T curve for a fixed amount of an ideal gas at constant volume is again a straight line. However, the shapes may vary if the constant parameters are also changed.
Now, answer the following questions:
Q.
Two moles of an ideal gas is changed from its initial state (16 atm, 6L) to final state (4 atm, 15L) in such a way that this change can be represented by a straight line in P - V curve. The maximum temperature attained by the gas during the above change is: (Take R = 1/12L atm K1 mo1-1)
When a sample of ideal gas is changed from an initial state to a final state, various curves can be plotted for the process like P - V curve, V - T curve, P - T curve etc.
For example, P - V curve for a fixed amount of an ideal gas at constant temperature is a rectangular hyperbola, V - T curve for a fixed amount of an ideal gas at constant pressure is a straight line and P - T curve for a fixed amount of an ideal gas at constant volume is again a straight line. However, the shapes may vary if the constant parameters are also changed.
Now, answer the following questions:
Q.
Which of the following graphs is not possible for a fixed amount of ideal gas upon moving from initial state A to final state B:
In the Figure, isotherms of CO2 at several temperatures near the critical point are shown. At the critical point (critical state), the distinction between the liquid and gaseous states disappear and the density of the gaseous substance is equal to that in the liquid state. For every gas this occurs at specific values of temperature and pressure, called critical temperature and critical pressure respectively. At temperatures and pressures above the critical point value, a gas is said be in a supercritical state. Critical constants are evaluated by solving the Vander W aals equation which is a cubic in volume. The values are Tc
In the supercritical region the behaviour is studied by plotting Z vs P plots. The variation in this region is studied with respect to boyles temperature a
At temperature
higher than CB the variation is linear (Plot I) and at temperature lower than CB the variation is non linear (Plot II) With reference to the passage answers the following questions:
Q.
For a real gas at a given temperature, which of the following facts is not correct?
In the Figure, isotherms of CO2 at several temperatures near the critical point are shown. At the critical point (critical state), the distinction between the liquid and gaseous states disappear and the density of the gaseous substance is equal to that in the liquid state. For every gas this occurs at specific values of temperature and pressure, called critical temperature and critical pressure respectively. At temperatures and pressures above the critical point value, a gas is said be in a supercritical state. Critical constants are evaluated by solving the Vander W aals equation which is a cubic in volume. The values are Tc
In the supercritical region the behaviour is studied by plotting Z vs P plots. The variation in this region is studied with respect to boyles temperature a
At temperature
higher than CB the variation is linear (Plot I) and at temperature lower than CB the variation is non linear (Plot II) With reference to the passage answers the following questions:
Q.
In the figure representing variation of the compressibility fac tor z of a real gas with pressure:
In the Figure, isotherms of CO2 at several temperatures near the critical point are shown. At the critical point (critical state), the distinction between the liquid and gaseous states disappear and the density of the gaseous substance is equal to that in the liquid state. For every gas this occurs at specific values of temperature and pressure, called critical temperature and critical pressure respectively. At temperatures and pressures above the critical point value, a gas is said be in a supercritical state. Critical constants are evaluated by solving the Vander W aals equation which is a cubic in volume. The values are Tc
In the supercritical region the behaviour is studied by plotting Z vs P plots. The variation in this region is studied with respect to boyles temperature a
At temperature
higher than CB the variation is linear (Plot I) and at temperature lower than CB the variation is non linear (Plot II) With reference to the passage answers the following questions:
Q.
A gas at C2° is condensed to liquid following the path XYAB. The liquid appears at the point:
Top Courses for JEE
Important Questions for Gaseous State MCQ- 1 (Advanced)
Gaseous State MCQ- 1 (Advanced)
Online Tests for Gaseous State MCQ- 1 (Advanced)
|
© EduRev
|
Education Revolution
|
|
