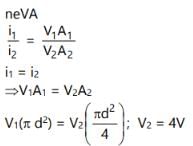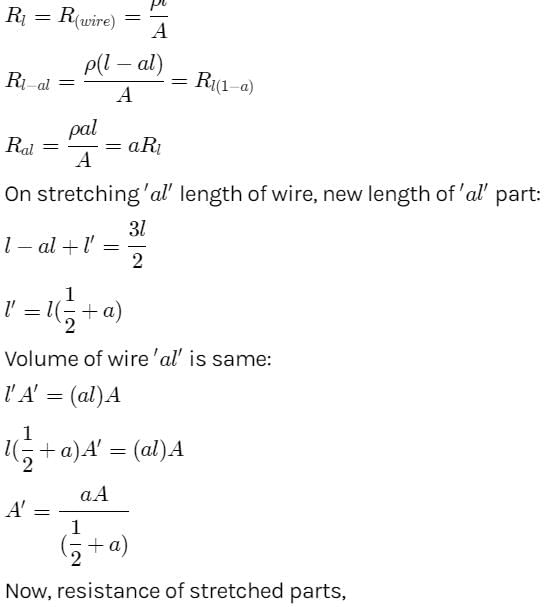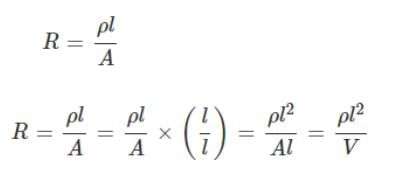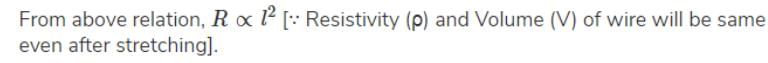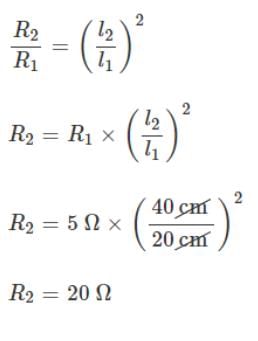HC Verma Test: Current Electricity - JEE MCQ
30 Questions MCQ Test - HC Verma Test: Current Electricity
The electric current in a liquid is due to the flow of
The electric current in a discharge tube containing a gas is due to
A current (I) flows through a uniform wire of diameter (d) when the mean drift velocity is V. The same current will flow through a wire of diameter d/2 made of the same material if the mean drift velocity of the electron is
When a potential difference (V) is applied across a conductor , the thermal speed of electrons is
A steady current is passing through a linear conductor of non-uniform cross-section. The current density in the conductor is
A metallic block has no potential difference applied across it. Then the mean velocity of free electron is
The resistance of some substances become zero at very low temperature , then these substances are called
The resistance of wire is 20W. The wire is stretched to three times its length. Then the resistance will now be
A hollow copper tube of 5 m length has got external diameter equal to 10 cm and the walls are 5 mm thick. If specific resistance of copper is 1.7 × 10-8 ohm × metre. calculate the resistance of the tube.
In order to increase the resistance of a given wire of uniform cross section to four times its value, a fraction of its length is stretched uniformly till the full length of the wire becomes times the original length what is the value of this fraction ?
A conductor with rectangular cross section has dimensions (a × 2a × 4a) as shown in figure. Resistance across AB is x, across CD is y and across EF is z. Then
A negligibly small current is passed through a wire of length 15 m and uniform cross-section 6.0×10-7 m2. The measured resistance of the wire is 5.0 W. The resistivity of the material is
The resistance of a wire of length 20 cm is 5W. It is stretched uniformly to a length of 40 cm. The resistance now becomes:
Two wires each of radius of cross section r but of different materials are connected together end to end (in series). If the densities of charge carriers in the two wires are in the ratio 1 : 4, the drift velocity of electrons in the two wires will be in the ratio.
In a wire of cross-section radius r, free electrons travel with drift velocity v when a current I flows through the wire. What is the current in another wire of half the radius and of the same material when the drift velocity is 2v ?
Read the following statements carefully :
Y : The resistivity of a semiconductor decreases with increases of temperature.
Z : In a conducting solid, the rate of collision between free electrons and ions increases with increase of temperature.
Select the correct statement from the following
A piece of copper and another of germanium are cooled from room temperature to 80K. The resistance of
An insulating pipe of cross-section area `A' contains an electrolyte which has two types of ions ® their charges being _e and +2e. A potential difference applied between the ends of the pipe result in the drifting of the two types of ions, having drift speed = v (_ve ion) and v/4 (+ ve ion). Both ions have the same number per unit volume = n. The current flowing through the pipe is
Two wires of the same material having radii in the ratio 1:2, carry currents in the ratio 4 : 1. The ratio of drift velocities of electrons in them is
A current I flows through a uniform wire of diameter d when the mean electron drift velocity is v. the same current will flow through a wire of diameter d/2 made of the same material if the mean drift velocity of the electron is
The current in a metallic conductor is plotted against voltage at two different temperatures T1 and T2. Which is correct
A uniform copper wire carries a current i amperes and has p carriers per metre3. The length of the wire is metres and its cross-section area is s metre2. If the charge on a carrier is q coulombs, the drift velocity in ms-1 is given by
In the presence of an applied electric field in a metallic conductor.
A wire has a non-uniform cross-section as shown in figure. A steady current flows through it. The drift speed of electrons at points P and q is vp and vQ.
A rectangular carbon block has dimensions 1.0 cm × 1.0 cm × 50 cm. Resistances are measured, first across two square ends and then across two rectangular ends, respectively. If resistivity of carbon is 3.5 × 10_5 W-m, then values of measured resistances respectively are :
A storage battery is connected to a charger for charging with a voltage of 12.5 Volts. The internal resistance of the storage battery is 1 W. When the charging current is 0.5 A, the emf of the storage battery is :
The terminal voltage across a battery of emf E can be
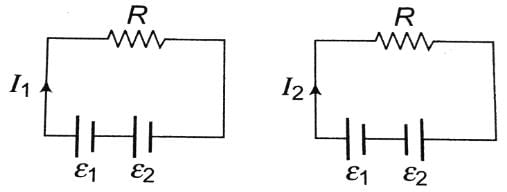
In order to determine the e.m.f of a storage battery it was connected in series with a standard cell in a certain circuit and a current I1 was obtained. When the battery is connected to the same circuit opposite to the standard cell a current I2 flow in the external circuit from the positive pole of the storage battery was obtained. What is the e.m.f e1 of the storage battery? The e.m.f of the standard cell is e2.
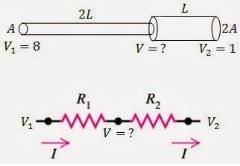
One end of a Nichrome wire of length 2L and cross-sectional area A is attatched to an end of another Nichrome wire of length L and cross-sectional area 2A. If the free end of the longer wire is at an electric potential of 8.0 volts, and the free end of the shorter wire is at an electric potential of 1.0 volt, the potential at the junction of the two wires is equal to