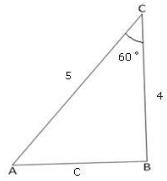
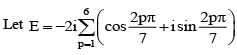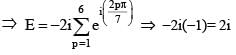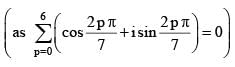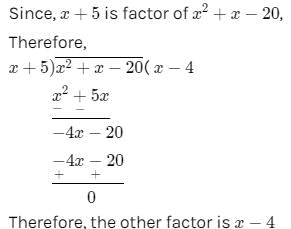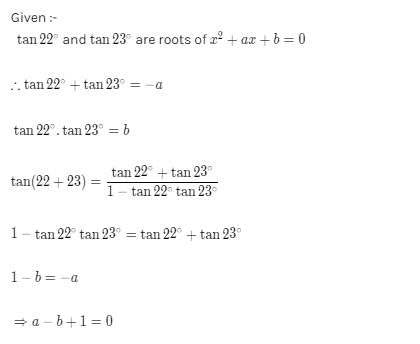HPSC PGT Mathematics Mock Test - 9 - HPSC TGT/PGT MCQ
30 Questions MCQ Test - HPSC PGT Mathematics Mock Test - 9
The present age of Annu and Raj are in ratio of 4 : 5. 8 years from now, the ratio of their age will be 5 : 6. Find their present age (in years):
Choose the alternative which is an odd word/number/letter pair out of the given alternatives.
What is the primary goal of the National Education Policy (NEP) 2020?
Which of the following is not a possible ordered pair for a matrix with 6 elements?
Let z and w be complex numbers such that and arg zω =π, then arg z =
Rolle’s Theorem is not applicable to the function f(x) = | x | for −2⩽x⩽2 because
In a room there are 2 green chairs, 3 yellow chairs and 4 blue chairs. In how many ways can Raj choose 3 chairs so that at least one yellow chair is included?
The set of values of p for which both roots of the equation 3x2 + 2x + p(p – 1) = 0 are of opposite sign is:
If the circle x2 + y2 = 9 touches the circle x2 + y2 + 6y + c = 0, then c is equal to
If z = x + yi ; x ,y ∈ R, then locus of the equation , where c ∈ R and b ∈ C, b ≠ 0 are fixed, is
The maximum value of (cos α1), (cos α2),........(cos αn) under the restrictions 0 < α1, α2,.......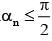 and (cot α1), (cot α2),..........(cot αn) = 1 is
and (cot α1), (cot α2),..........(cot αn) = 1 is
A parabola whose axis is along the y-axis, vertex is (0,0) and point from the first and second quadrants lie on it, has the equation of the type
The point from which the tangents to the circles x2 + y2 – 8x + 40 = 0, 5x2 + 5y2 – 25 x + 80 = 0, x2 + y2 – 8x + 16y + 160 = 0 are equal in length is
In answering a question on a multiple choice test, a student either knows the answer or guesses. Let 3/4 be the probability that he knows the answer and 1/4 be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability 1/4. What is the probability that the student knows the answer given that he answered it correctly?
If one of the factor of x2 + x – 20 is (x + 5). Find the other
The number of ways in which a necklace can be formed by using 5 identical red beads and 6 identical white beads is:
tan 22o and tan 23o are roots of x2 + ax + b = 0 then
If A and B are disjoint, then n (A ∪ B) is equal to:
If t0, t1, t2, ............tn are the consecutive terms in the expansion (x + a)n then (t0 - t2 + t4 - t6 + ....)2 + (t1 - t3 + t5....)2 =
The area enclosed by the parabola y2 = 2x and its tangents through the point (-2 , 0) is
If f (x + y) = 2f (x) f (y) for all x, y ∈ R where f ' (0) = 3 and f (4) = 2, then f ' (4) is equal to



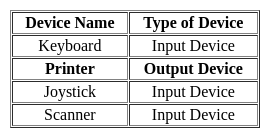
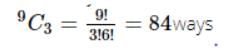
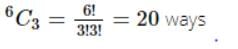
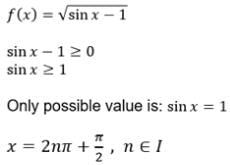
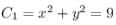
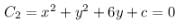
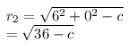

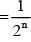 [sin 2α1. sin2α2 .........sin 2αn]
[sin 2α1. sin2α2 .........sin 2αn]