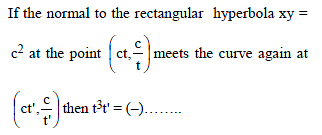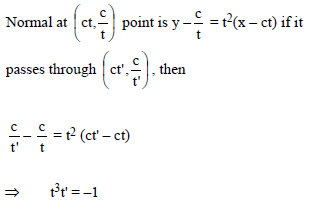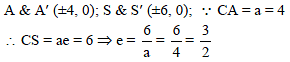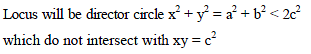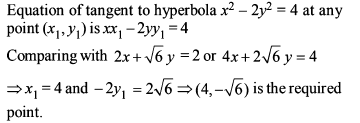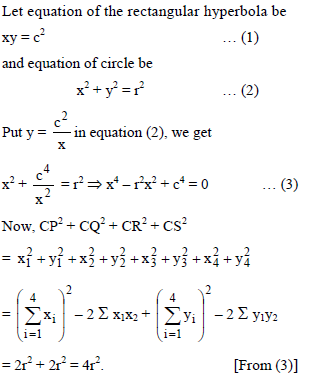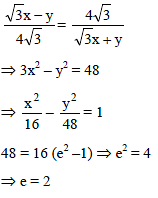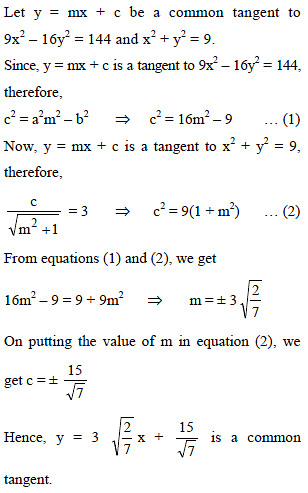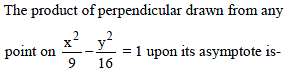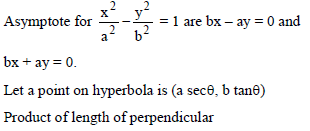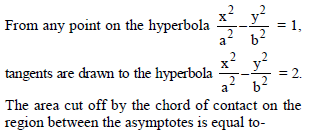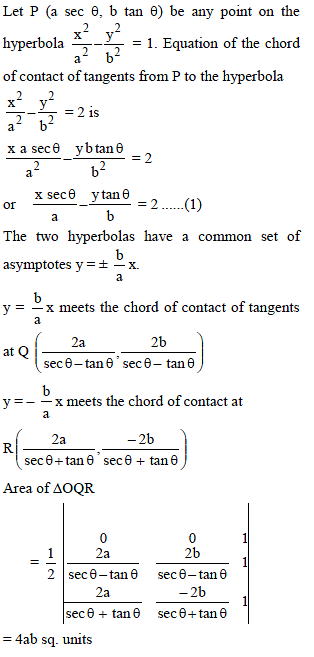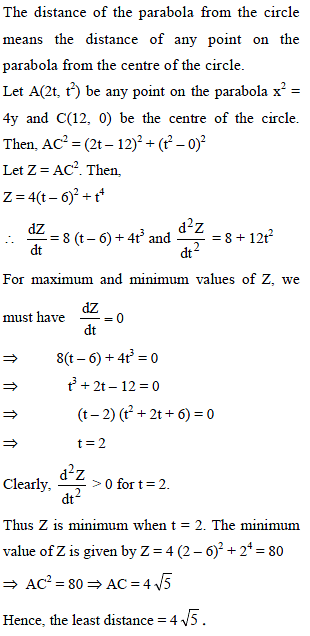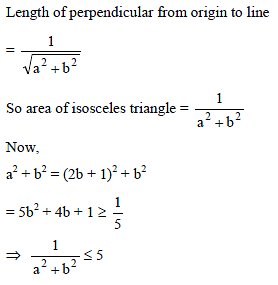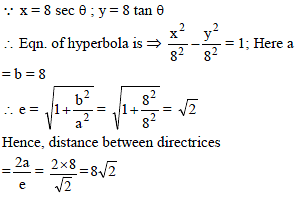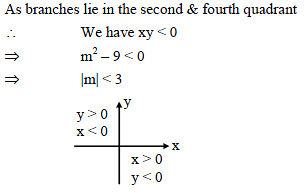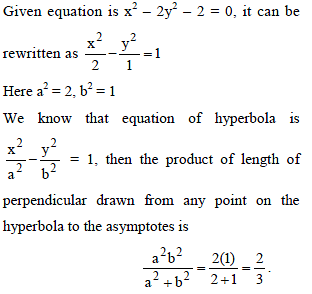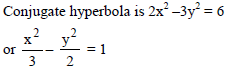Hyperbola - 1 - JEE MCQ
29 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Hyperbola - 1
Equation of the chord of the hyperbola 25x2 - 16y2 = 400, which is bisected at the point (6, 2) is
The equation of the transverse and conjugate axes of a hyperbola are respectively x + 2y – 3 = 0, 2x – y + 4 = 0 and their respective lengths are √2 and 2/√3. The equation of the hyperbola is
A hyperbola, having the transverse axis of length 2 sin θ, is confocal with the ellipse 3x2 + 4y2 = 12. Then its equation is:
The number of tangents and normals to the hyperbola of the slope 1 is
If (4, 0) and (–4, 0) be the vertices and (6, 0) and (–6, 0) be the foci of a hyperbola, then its eccentricity is-
If centre, vertex & focus of hyperbola are (2, 0) (4, 0) & (8, 0) then length of latus rectum
Consider the set of hyperbola xy = k, k ∈ R. Let e1 and e2 be the eccentricities when k = 16 and k = 25 respectively then the value of e12 – e22 equals -
A rectangular hyperbola whose centre is C is cut by any circle of radius r in four points P, Q, R and S. then CP2 + CQ2 + CR2 + CS2 is equal to -
PM and PN are the perpendiculars from any point on a rectangular hyperbola to its asymptotes. If Q divides MN in the ratio 3 : 1, then the locus of Q is -
From any point on a hyperbola xy = c2 tangents are drawn to another hyperbola xy = a2 which has the same asymptotes. Then the chord of contact cuts off a constant area from the asymptotes:
A point P moves in such a way that the sum of the slopes of the normals drawn from itto the hyperbola xy = 4 is equal to the sum of the ordinates of feet of the normals. The locus of P is a parabola x2 = 4y. Then the least distance of this parabola from the circle x2 – y2 – 24x + 128 = 0 is -
Let ax + by = 1 be a chord of the curve 3x2 – y2 – 2x + 4y = 0 intersecting the curve at the points A and B such that AB subtends a right angle at the origin O. If the triangle OAB is isosceles then the area of Δ cannot exceed
The distance between the directrices of the hyperbola x = 8 sec θ, y = 8 tan θ is-
If xy = m2 – 9 be a rectangular hyperbola whose branches lie only in the second and fourth quadrant, then -
The product of the lengths of perpendiculars drawn from any point on the hyperbola x2 – 2y2 – 2 = 0 to its asymptotes, is -
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|


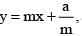 a = 2 and c2 = a2m2 - b2
a = 2 and c2 = a2m2 - b2