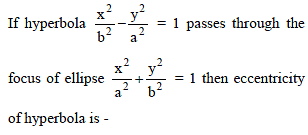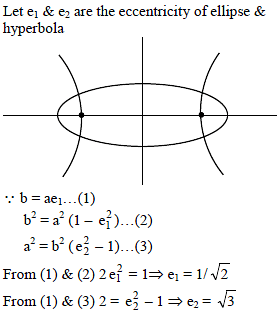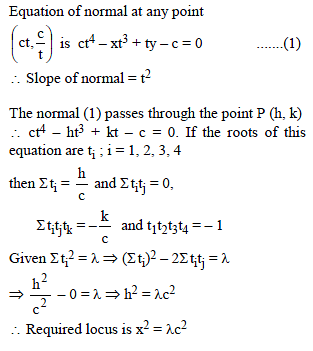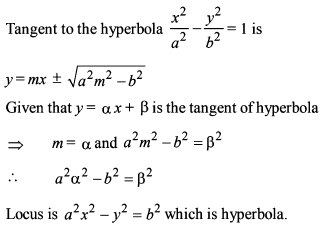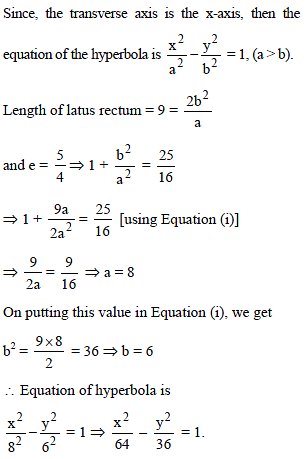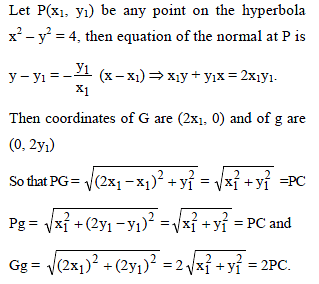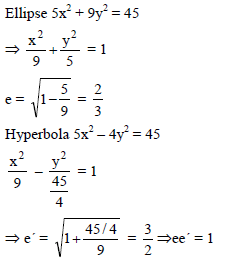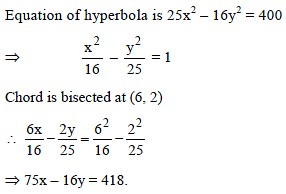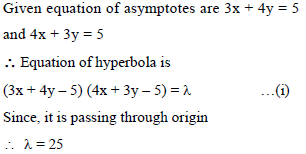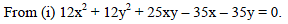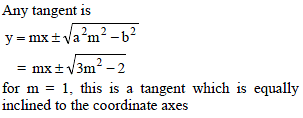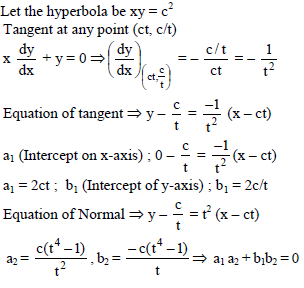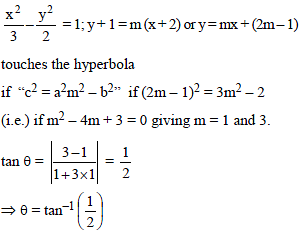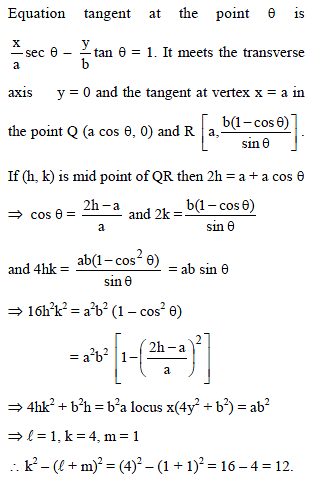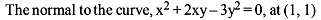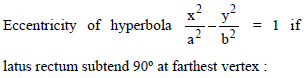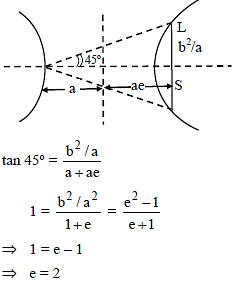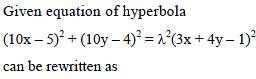Hyperbola - 2 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Hyperbola - 2
Locus of the feet of the perpendiculars drawn from either foci on a variable tangent to the hyperbola 16y2 – 9x2 = 1 is
The coordinates of the point of intersection of two tangents to a rectangular hyperbola referred to its asymptote as axes are -
If the sum of the squares of slopes of the normals from a point P to the hyperbola xy = c2 is equal to λ (λ ∈ R+), then the locus of the point P is–
The equation of the hyperbola in the standard form (with transverse axis along the x-axis) having the length of the latus rectum = 9 unit and eccentricity = 5/4 , is -
If the normal at P to the rectangular hyperbola x2 – y2 = 4 meets the axis in G and g and C is the centre of the hyperbola, then -
If e and e´ are the eccentricities of the ellipse 5x2 + 9y2 = 45 and the hyperbola 5x2 – 4y2 = 45 respectively, then ee´ =
Equation of the chord of the hyperbola 25x2 – 16y2 = 400 which is bisected at the point (6, 2), is -
Equation of hyperbola passing through origin and whose asymptotes are 3x + 4y = 5 and 4x + 3y = 5, is -
If the tangent and the normal to a rectangular hyperbola at a point cut off intercepts a1, a2 on one axis and b1, b2 the other axis then a1a2 + b1b2 is equal to-
The angle between the tangents from (–2, –1) to the hyperbola 2x2 – 3y2 = 6 is-
At the point of intersection of the rectangular hyperbola xy = c2 and the parabola y2 = 4ax tangents to the rectangular hyperbola and the parabola make an angle θ and ϕ respectively with x- axis, then–
If P is a point on the hyperbola 16x2 – 9y2 = 144 whose foci are S1 and S2, then PS1 ~ PS2 =
Tangents PA and PB are drawn to circle (x + 4)2 + (y – 4)2 =1 from variable points P on xy = 1. The locus of circumcentre of the triangle PAB is:
If equation (10x – 5)2 + (10y – 4)2 = λ2 (3x + 4y – 1)2 represents a hyperbola, then -
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|