IIFT Data Interpretation MCQ Quiz - 4 - CAT MCQ
18 Questions MCQ Test - IIFT Data Interpretation MCQ Quiz - 4
The following bar chart gives the percentage growth in the number of households in the middle, upper middle and high income categories in the four regions for the period from 1987-88 to 1994-95

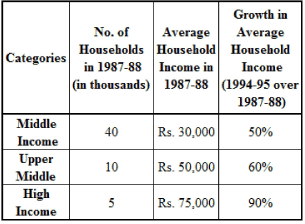
Additional directions for the last two questions of this set:
If the same data as the above were used, with the additional information that the numbers of households in each category were equally distributed in all the regions then
Q.
Which region showed the highest growth rate in the number of households in all the income categories for the period?
The following bar chart gives the percentage growth in the number of households in the middle, upper middle and high income categories in the four regions for the period from 1987-88 to 1994-95


Additional directions for the last two questions of this set:
If the same data as the above were used, with the additional information that the numbers of households in each category were equally distributed in all the regions then
Q.
What was the total household income in the Northern Region for the upper middle class?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The following bar chart gives the percentage growth in the number of households in the middle, upper middle and high income categories in the four regions for the period from 1987-88 to 1994-95


Additional directions for the last two questions of this set:
If the same data as the above were used, with the additional information that the numbers of households in each category were equally distributed in all the regions then
Q.
What is the percentage increase in the total number of households for the Northern Region (upper middle) over the given period?
The following bar chart gives the percentage growth in the number of households in the middle, upper middle and high income categories in the four regions for the period from 1987-88 to 1994-95
Additional directions for the last two questions of this set:
If the same data as the above were used, with the additional information that the numbers of households in each category were equally distributed in all the regions then
Q.
What was the average income of the high-income group in 1987-88?
The following bar chart gives the percentage growth in the number of households in the middle, upper middle and high income categories in the four regions for the period from 1987-88 to 1994-95
Additional directions for the last two questions of this set:
If the same data as the above were used, with the additional information that the numbers of households in each category were equally distributed in all the regions then
Q.
The ratio of total income for the high income category to the upper middle class increased by how much ercent in the given period?
The following bar chart gives the percentage growth in the number of households in the middle, upper middle and high income categories in the four regions for the period from 1987-88 to 1994-95
Additional directions for the last two questions of this set:
If the same data as the above were used, with the additional information that the numbers of households in each category were equally distributed in all the regions then
Q.
The average income for the Northern region in 1987-88, was _____ .
Owing to a global economic slowdown the company Testa Ltd. has decided to review its employee compensation structure in order to cut costs. In the existing structure all 100 employees are paid a Fixed Salary (FS) equal to 10000 and a Variable Salary (VS), where the Variable Salary depends upon the performance of the company and is decided as a percentage of the Fixed Salary.
Employee salary = FS + VS The company is thinking of changing it into a variable pay structure where different groups of employees are paid as shown in the table below
Where the Variable Salary depends on the company performance and is calculated as a percentage of Fixed salary.
Q.
The company does not perform satisfactorily and decides on a variable salary = 10% of fixed salary. What is the percentage gain/loss of the company if it uses the new structure with respect to the existing compensation structure?
Owing to a global economic slowdown the company Testa Ltd. has decided to review its employee compensation structure in order to cut costs. In the existing structure all 100 employees are paid a Fixed Salary (FS) equal to 10000 and a Variable Salary (VS), where the Variable Salary depends upon the performance of the company and is decided as a percentage of the Fixed Salary.
Employee salary = FS + VS The company is thinking of changing it into a variable pay structure where different groups of employees are paid as shown in the table below
Where the Variable Salary depends on the company performance and is calculated as a percentage of Fixed salary.
Q.
If the variable salary is decided as 15% of the fixed salary in the existing compensation structure, what should be the percentage variable pay in the new compensation structure such that there is no difference in total employee compensation between both the structures?
Owing to a global economic slowdown the company Testa Ltd. has decided to review its employee compensation structure in order to cut costs. In the existing structure all 100 employees are paid a Fixed Salary (FS) equal to 10000 and a Variable Salary (VS), where the Variable Salary depends upon the performance of the company and is decided as a percentage of the Fixed Salary.
Employee salary = FS + VS The company is thinking of changing it into a variable pay structure where different groups of employees are paid as shown in the table below
Where the Variable Salary depends on the company performance and is calculated as a percentage of Fixed salary.
Q.
The company is not satisfied with the cost savings from the new compensation structure and decides to retrench 9 employees from employee categories of A and B such that employees retrenched from category Marks A is twice those retrenched from category B. The variable pay for the new compensation is declared to be 10%. What should be the percentage variable pay in the old compensation structure such that there is no difference between the two?
Owing to a global economic slowdown the company Testa Ltd. has decided to review its employee compensation structure in order to cut costs. In the existing structure all 100 employees are paid a Fixed Salary (FS) equal to 10000 and a Variable Salary (VS), where the Variable Salary depends upon the performance of the company and is decided as a percentage of the Fixed Salary.
Employee salary = FS + VS The company is thinking of changing it into a variable pay structure where different groups of employees are paid as shown in the table below
Where the Variable Salary depends on the company performance and is calculated as a percentage of Fixed salary.
Q.
If the total variable salary component of category A employees is equal to the total salary of category C employees, in the new system, then what percentage of the fixed salary is the variable salary?
The two pie-charts below provide information about the background-wise batch distribution of a B-school class in 2011 and 2012. The total number of students from the Arts background increased by 25% in 2012 as compared to 2011. (Assume that the total number of students to be 300 in the year 2011)
Q.
How many more students were there from the Humanities background in 2012 as compared to 2011 ?
The two pie-charts below provide information about the background-wise batch distribution of a B-school class in 2011 and 2012. The total number of students from the Arts background increased by 25% in 2012 as compared to 2011. (Assume that the total number of students to be 300 in the year 2011)
Q.
What was the percentage increase in the number of students from the Science background in 2012 as compared to 2011 ?
The bar graph below shows the average electricity consumption in a house in all alternate years from 2000 to 2008. The payable amount for a particular year comprises the billed amount and 12.36% service tax. The service tax is calculated on the billed amount. The billed amount is calculated solely on the number of units consumed, and the units are billed as per various slabs (as shown in the table). For instance, if a household has consumed 420 units in a year, the first 100 units are charged at Rs. 2.23/unit, the next 300 emits are charged at Rs. 4.78/unit and the final 20 emits are charged at Rs. 6.78/unit.
Q.
What is the payable amount for this household in 2006?
The bar graph below shows the average electricity consumption in a house in all alternate years from 2000 to 2008. The payable amount for a particular year comprises the billed amount and 12.36% service tax. The service tax is calculated on the billed amount. The billed amount is calculated solely on the number of units consumed, and the units are billed as per various slabs (as shown in the table). For instance, if a household has consumed 420 units in a year, the first 100 units are charged at Rs. 2.23/unit, the next 300 emits are charged at Rs. 4.78/unit and the final 20 emits are charged at Rs. 6.78/unit.
Q.
By what amount does the payable amount for 2004 exceed the payable amount for 2002?
The bar graph below shows the average electricity consumption in a house in all alternate years from 2000 to 2008. The payable amount for a particular year comprises the billed amount and 12.36% service tax. The service tax is calculated on the billed amount. The billed amount is calculated solely on the number of units consumed, and the units are billed as per various slabs (as shown in the table). For instance, if a household has consumed 420 units in a year, the first 100 units are charged at Rs. 2.23/unit, the next 300 emits are charged at Rs. 4.78/unit and the final 20 emits are charged at Rs. 6.78/unit.
Q.
How much service tax has the household paid in all over the given period?
The table below shows the number of male and female voters in eight constituencies of a state from 2012 to 2014.
Q.
In how many constituencies is the compound annual growth rate (CAGR) of male voters less than that of the female voters?
The table below shows the number of male and female voters in eight constituencies of a state from 2012 to 2014.
Q.
Which constituency witnessed the highest percentage growth in the total number of voters, over the given period?
The table below shows the number of male and female voters in eight constituencies of a state from 2012 to 2014.
Q.
In which constituency is the CAGR of total voters the least over the given period?

















