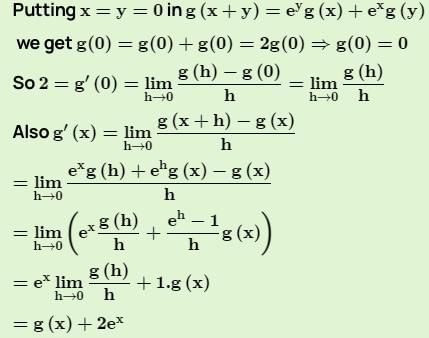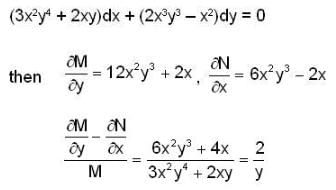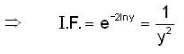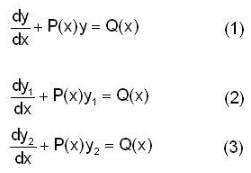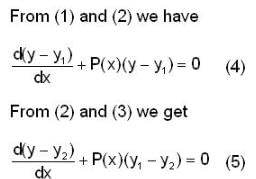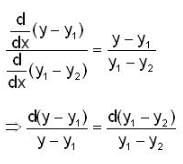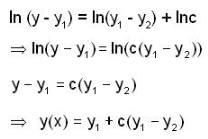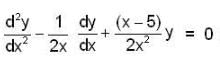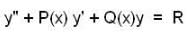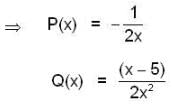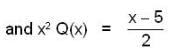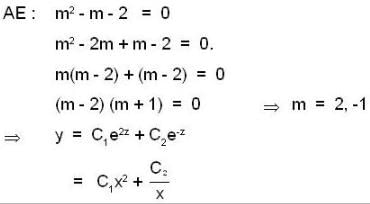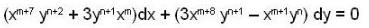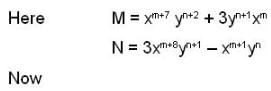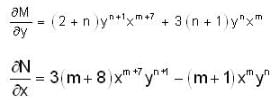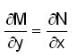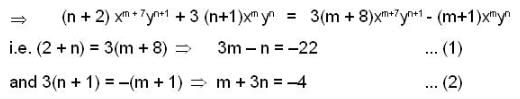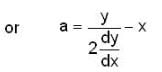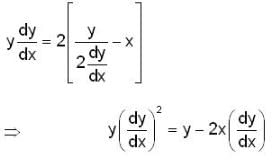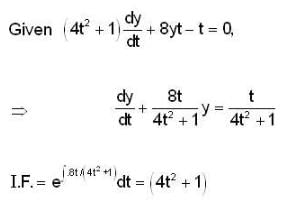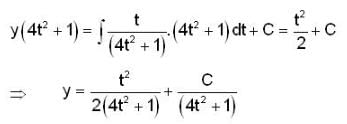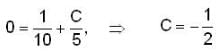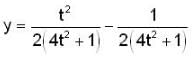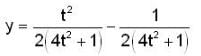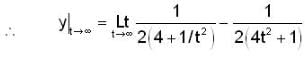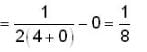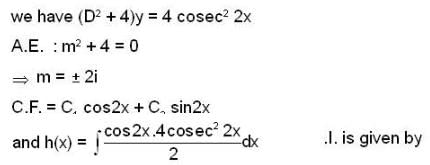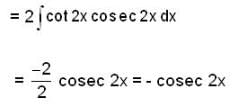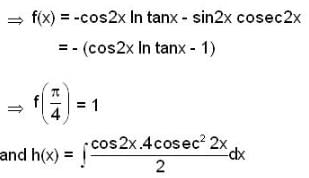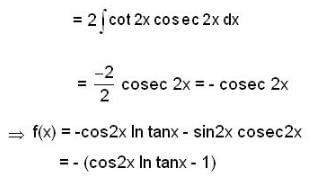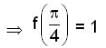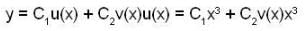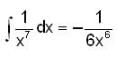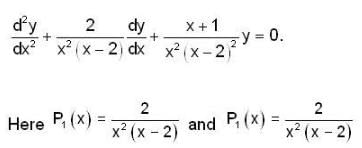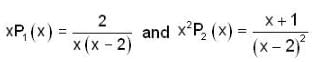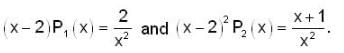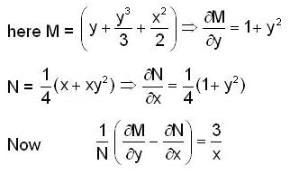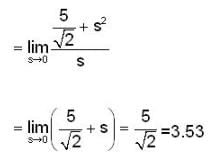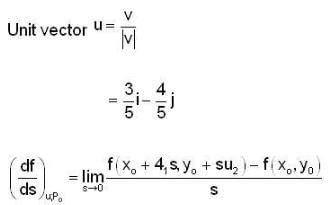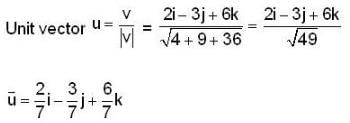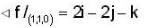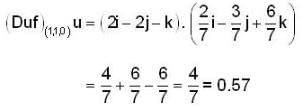IIT JAM Mathematics Practice Test- 1 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 1
Let ( y - C)2 = Cx be the primitive of  The no. of integral curves which will pass through (1, 2) is,
The no. of integral curves which will pass through (1, 2) is,
 The no. of integral curves which will pass through (1, 2) is,
The no. of integral curves which will pass through (1, 2) is,Which of the following transformations reduce the differential equation 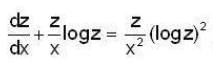 into the form
into the form 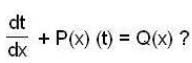
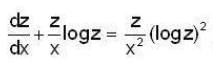 into the form
into the form 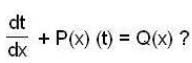
The solution of the differential equation 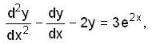
where y(0) = 0 and y'(0) = -2 is
An integrating factor of the differential equation 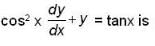
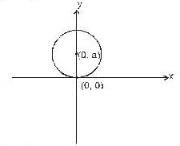
The differential equation representing the family of circles touching x-axis at the origin is
A curve passing through (2,3) and satisfying the differential equation
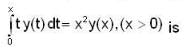
The differential equation
(3a2x2 + by cos x)dx + (2 sin x - 4ay3)dy = 0 is exact for
The integrating factor of the equation (1 + y2)dx = (tan-1y - x)dy is -
The slope of a curve at any point is the reciprocal of twice the ordinate at the point and it passes through the point (4, 3). The equation of the curve is
If (c1 logx + c2)x2 is the general solution of the differential equation 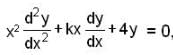 then k equals
then k equals
Consider a function g which has derivative g’(x) for every real x and which satisfies g’(0) = 2 and g(x + y) = ey g(x) + ex g(y) for all x and y. Then which of the followings is/are correct ?
Consider the differential equation (3x2y4 + 2xy)dx+(2x3y3 - x2)dy=0 then which of the follwing(s) is/are not an I.F
If y1 and y2 are two solution of the differential equation 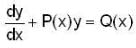 . Then which of the followings can be given as general soln of this differential eqn.
. Then which of the followings can be given as general soln of this differential eqn.
For the given differential equation, which of the following(s) statement are true,
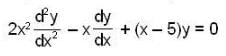
Given that φ(x) = x2 is a solution of the differential equation, 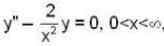 then which of the following(s) is/are not its 2nd L.l. solution.
then which of the following(s) is/are not its 2nd L.l. solution.
If the integrating factor of the differential equation, (x7y2 + 3y)dx + 3x8y - x) dy = 0 is of the form xmyn , then the sum of value of m and n is __________.
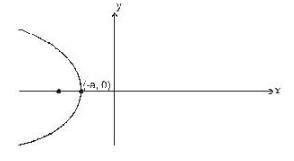
The sum of order and degree of the differential equation representing the family o f parabolas whose center is (-a.O) i s _______ .
The value o f y as t -> ∞ , for an initial value o f y(1) = 0, for the differential equation
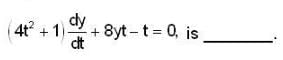
If y = f(x) be a particular solution of differential equation y" + 4y = 4 cosec2 2x , then f(x) at 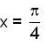 is _________.
is _________.
Consider the differential equation 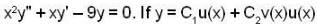 be its general solution and u(x) = x3 then the value of v(x) at x=(-1) is, _________
be its general solution and u(x) = x3 then the value of v(x) at x=(-1) is, _________
No. of regular Singular points of the differential equation, x2( x - 2 )2 y" + 2x (x - 2) y’+ (x + 1)y = 0. is __________.
The value of I.F of the differential equation, 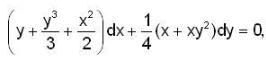 at x = 2 is, _______.
at x = 2 is, _______.
The directional derivative of f(x,y) = x2 + xy at Po(1,2) in the direction of the unit vector 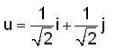
Find the directional Derivative of f(x,y) = x2 sin 2y at the point 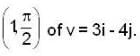
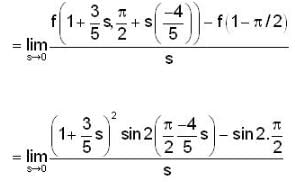
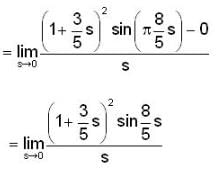
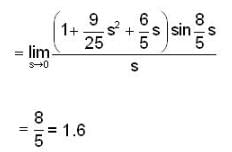
Find the derivation of f(x,y,z) = x3 - xy2 -z at Po (1,1,0) in the direction of v= 2i - 3j+ 6k


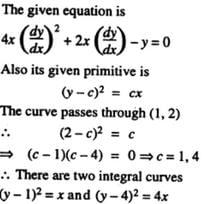
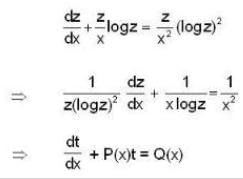
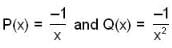 which shows that the transformation t= 1/log z
which shows that the transformation t= 1/log z 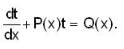

 has a solution ___________, when t= 0, then
has a solution ___________, when t= 0, then 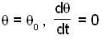
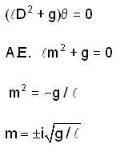
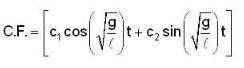
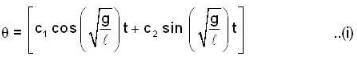
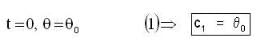
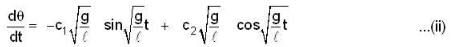
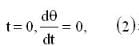
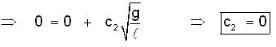
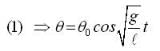


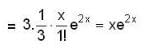
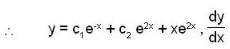
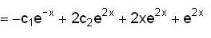
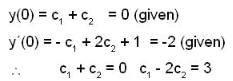
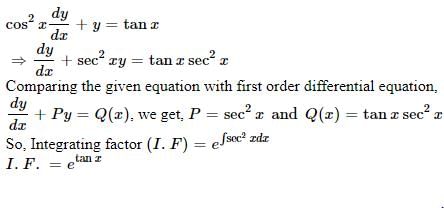
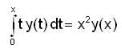
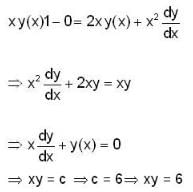
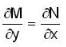


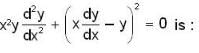
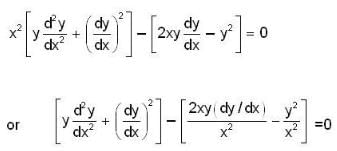

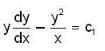
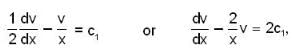 which is linear. Its I.F =
which is linear. Its I.F = 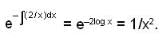
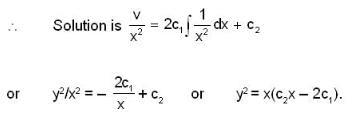
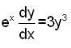 , given y(0) = 1/2 is
, given y(0) = 1/2 is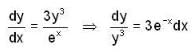
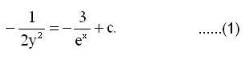
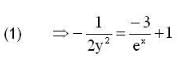

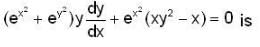
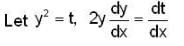
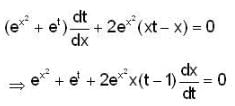
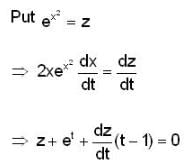

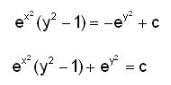
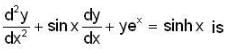
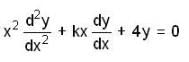 --(1)
--(1)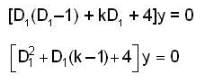
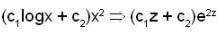
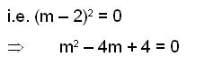 ... (4)
... (4)