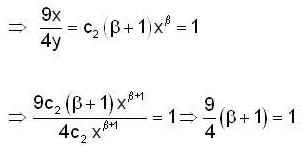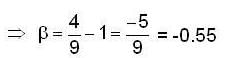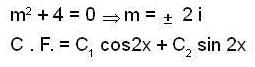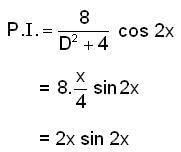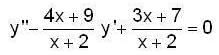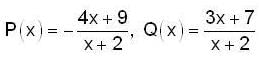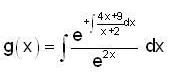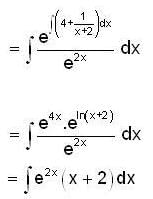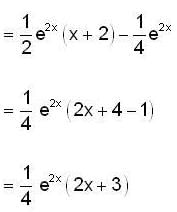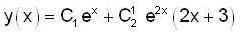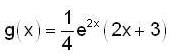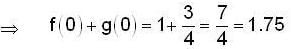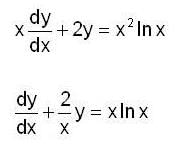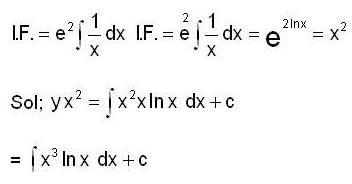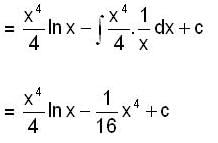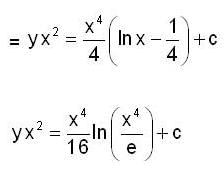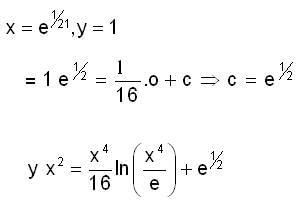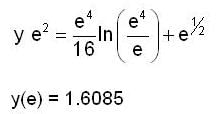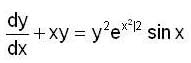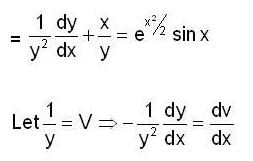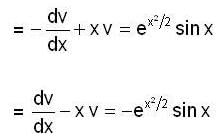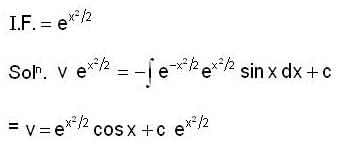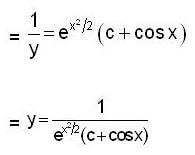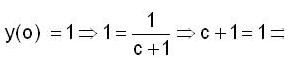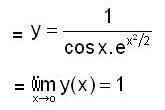IIT JAM Mathematics Practice Test- 4 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 4
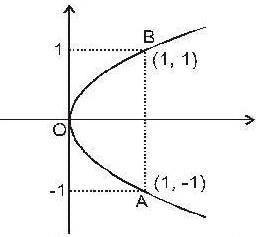
Compute the integral 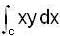 along the arc of the parabola x = y2 from (1,-1) to (1,1)
along the arc of the parabola x = y2 from (1,-1) to (1,1)
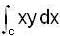 along the arc of the parabola x = y2 from (1,-1) to (1,1)
along the arc of the parabola x = y2 from (1,-1) to (1,1)Evaluate the integral 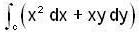 taken along the quarter circle x = cos t, y = sin t, joining the same points.
taken along the quarter circle x = cos t, y = sin t, joining the same points.
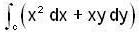 taken along the quarter circle x = cos t, y = sin t, joining the same points.
taken along the quarter circle x = cos t, y = sin t, joining the same points.By changing the order of integration, the integral 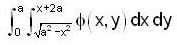 can be represented as
can be represented as 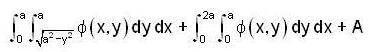 determine the value of A.
determine the value of A.
Evaluate 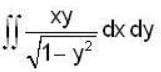 over the positive quadrant of the circle x2 + y2 = 1 .
over the positive quadrant of the circle x2 + y2 = 1 .
Let R be the image of the triangular region S with vertices (0, 0) (0,1) is uv-plane under the transformation x = 2u - 3v and y = u + v.
Then 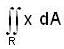 equals
equals
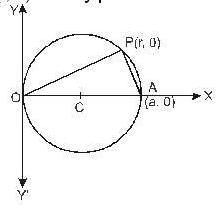
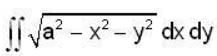 over the semicircle x2 + y2 = ax in the positive quadrant is equal to -
over the semicircle x2 + y2 = ax in the positive quadrant is equal to -
An integrating factor for the differential equation (cos y sin 2x) dx + (cos2y - cos2x ) dy = 0 is,
Let 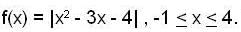 then, which of the follwing is not true ?
then, which of the follwing is not true ?
Let y(x) be the solution of initial value problem,
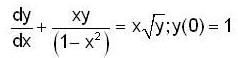
The y(1) is equal to,
Let F(x) be the particular integral of the differential equation y" + y = (x - cot x) If there exist c e R such that F(c) = c, then c is equal to,
Let y(x) be the solution of the differential equation,
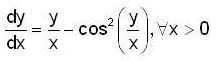
Satisfying the condition 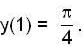 Then which o f the following is/are
Then which o f the following is/are
If f(x) is defined [ -2,2 ] by / ( x ) = 4x2 - 3x +1 and 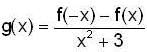 then
then
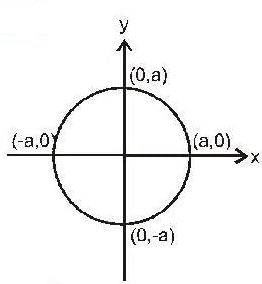
If the equation of the curve is x2 + y2 = a2 then
Evaluate 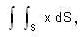 where S is the entire surface of the solid bounded by the cylinder x2 + y2 =1 and the planes z = 0, z = x + 2.
where S is the entire surface of the solid bounded by the cylinder x2 + y2 =1 and the planes z = 0, z = x + 2.
The value of 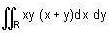 over the area between the parabola y - x2 and the line y = x is ______.
over the area between the parabola y - x2 and the line y = x is ______.
Evaluate the integral 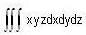 over the volume enclosed by three coordinate planes and the plane x + y + z = 1.
over the volume enclosed by three coordinate planes and the plane x + y + z = 1.
Evaluate 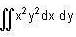 over the domain {(x, y ) : x ≥ 0, y ≥ 0, x2 + y2 ≤ 1}.
over the domain {(x, y ) : x ≥ 0, y ≥ 0, x2 + y2 ≤ 1}.
If the orthogenal trajectories of the family of ellipse 9x2 + 4y2 = c1 where c1 > 0 are given by 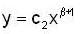 where c2 ∈ R , then the value of β i s ..... ( conect upto two decimal places).
where c2 ∈ R , then the value of β i s ..... ( conect upto two decimal places).
Consider the differential equation y" + 4y = 8cos2x , with y(0) = 0 and 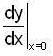 then y( π ) is equal to _________ .
then y( π ) is equal to _________ .
Let y(x) = c1 f(x) + c2 g(x) be the general solution of (x + 2) y" - (4x + 9)y' + (3x + 7)y = 0, then f(0) + g(0) is equal to _________.
Consider the differential equation 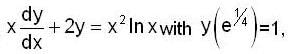 then y(e) is equal to
then y(e) is equal to
Let y(x) is a solution of differential equation 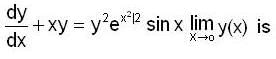 equal to. satisfying y(o) = 1. then
equal to. satisfying y(o) = 1. then


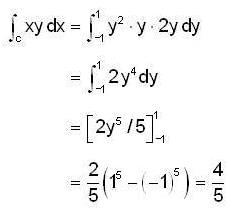
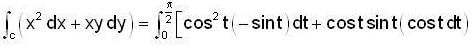


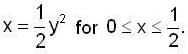 Assume that y is positive
Assume that y is positive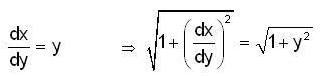
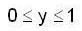
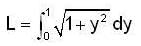
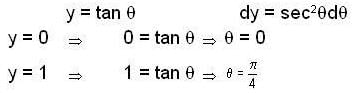
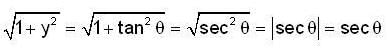
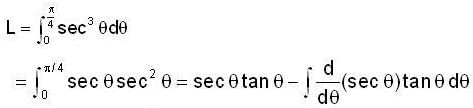

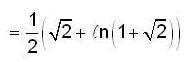
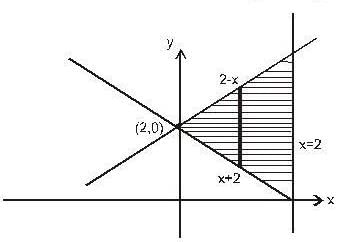
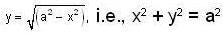 and the straigh t line y = x + 2a. The limits of x are given by the straigh t lines x = 0 and x = a
and the straigh t line y = x + 2a. The limits of x are given by the straigh t lines x = 0 and x = a
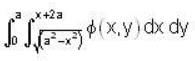


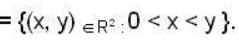 Then
Then 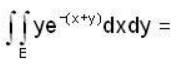
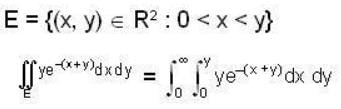

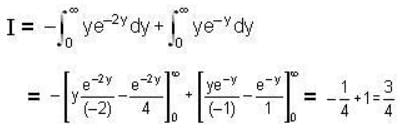
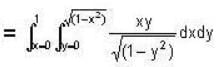
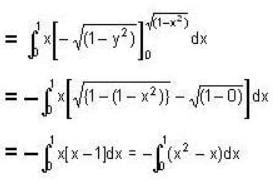
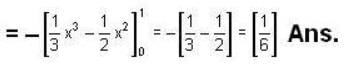
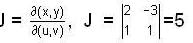
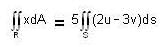
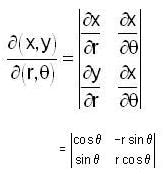
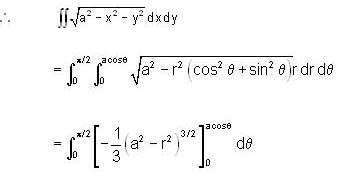
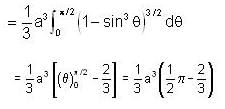

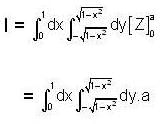
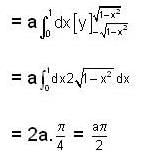
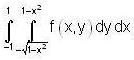 gives
gives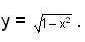


 and for area AOCD upper and lower limits of x is
and for area AOCD upper and lower limits of x is 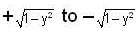 and limits of y is O to -1
and limits of y is O to -1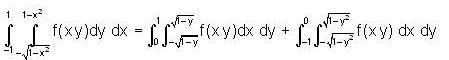
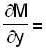 - sin y sin 2x
- sin y sin 2x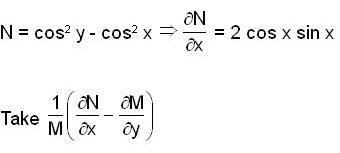
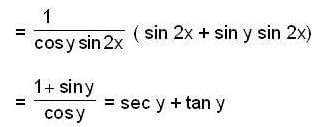
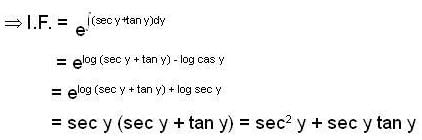
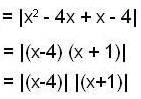
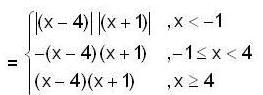
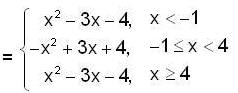
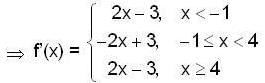
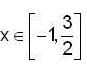
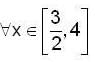
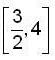
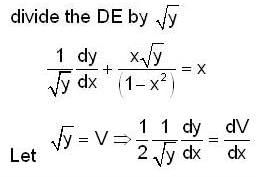
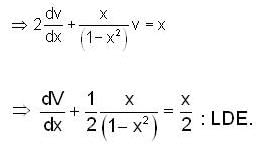
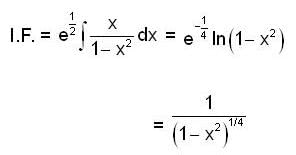
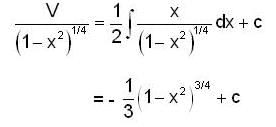 Given y(0) = 1
Given y(0) = 1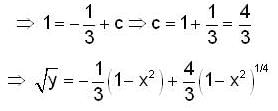
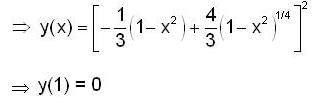

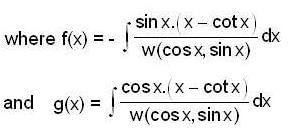
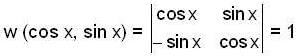
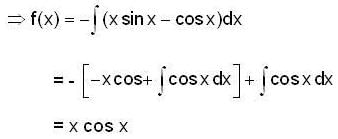

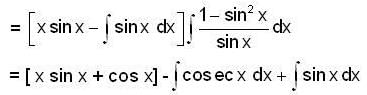
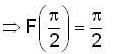
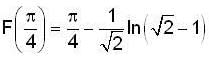
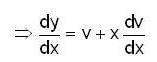
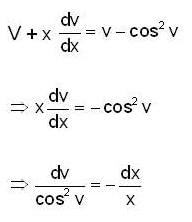
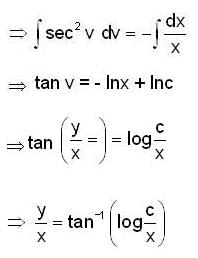
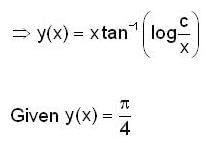
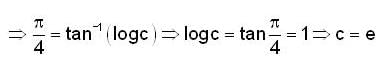
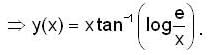
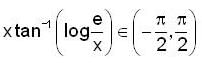 : bounded But x not bounded.
: bounded But x not bounded.

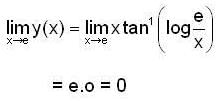

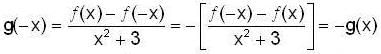
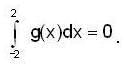
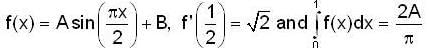 then
then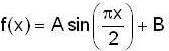
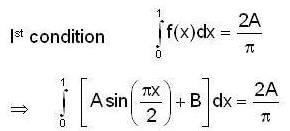
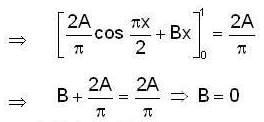
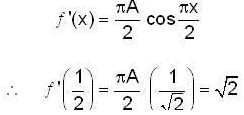
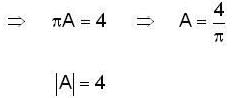
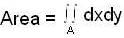

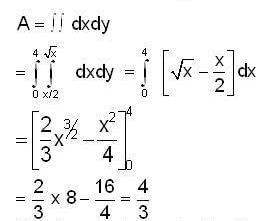
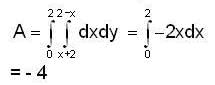
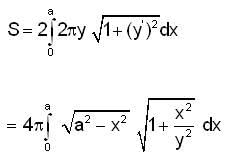
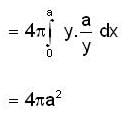
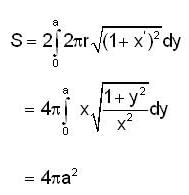
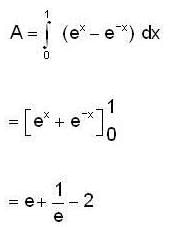
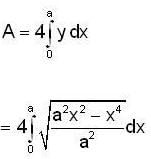
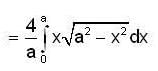
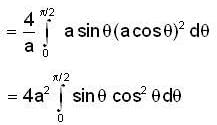
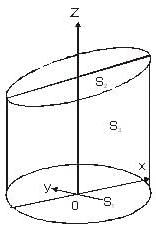
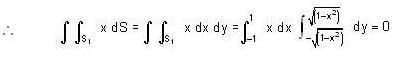
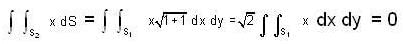
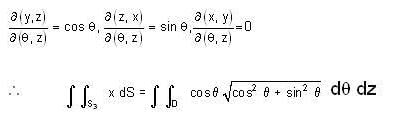 where D is the corresponding domain in the θ z- plane.
where D is the corresponding domain in the θ z- plane.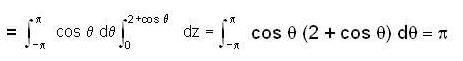
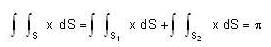
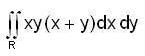
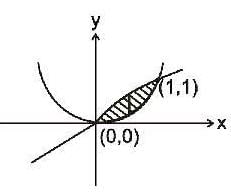
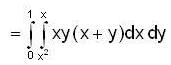
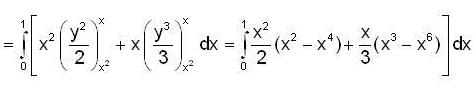
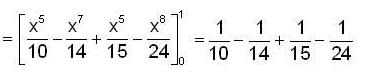
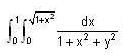 is ___________.
is ___________.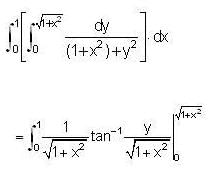
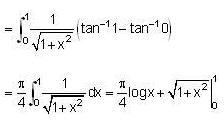
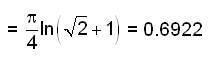
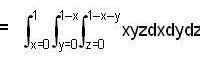
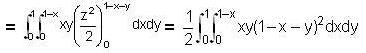
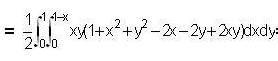
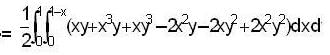
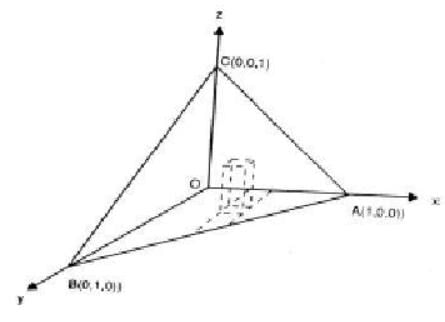
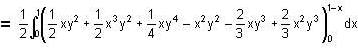
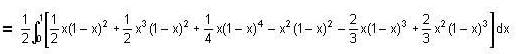
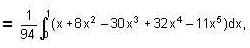
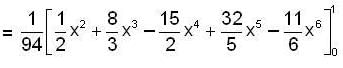
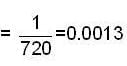
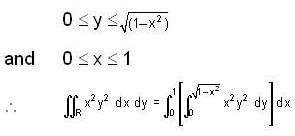
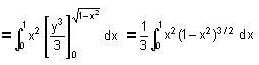
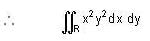
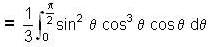
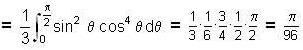
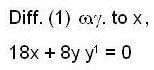
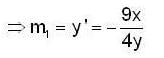 .. (2)
.. (2)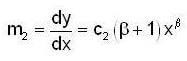 ... (4)
... (4)