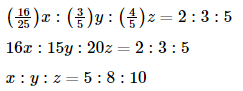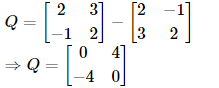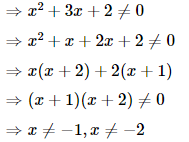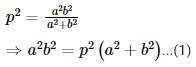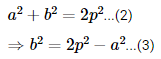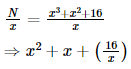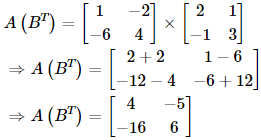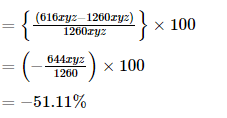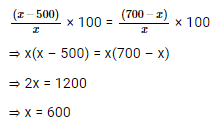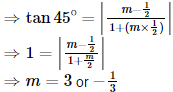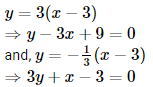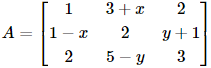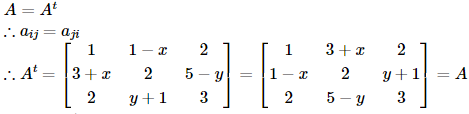IPMAT Mock Test - 7 (New Pattern) - Commerce MCQ
30 Questions MCQ Test - IPMAT Mock Test - 7 (New Pattern)
Find the average of first three odd multiples of 9.
A train x running at 74 km/h crosses another train y running at 52 km/h in the opposite direction in 12 seconds. If the length of y is two-thirds that of x, then what is the length of y (in m)?
Direction: Study the given bar graph carefully and answer the questions given below.
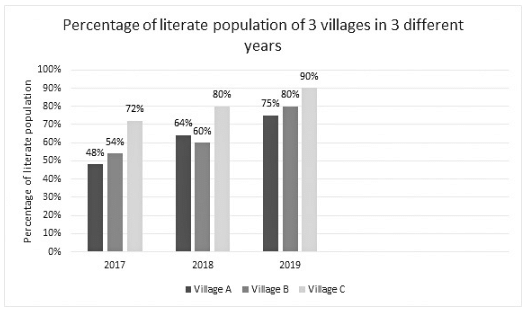
Q. In the year 2015, the total number of literates in the three villages is 285000. If the population of village A and B in the year 2015 is 125000 and 150000 respectively, then what is the population of the village C in the year 2015?
Direction: Study the given bar graph carefully and answer the questions given below.
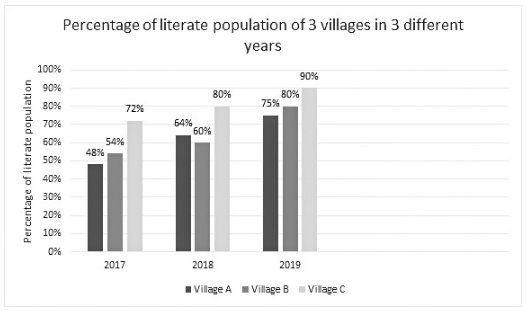
Q. In the year 2017, if the number of literate males in village A is 42000 more than the number of literate females, then find the ratio of the number of literate males to the number of literate females in village A in 2017.
Direction: Study the given bar graph carefully and answer the questions given below.
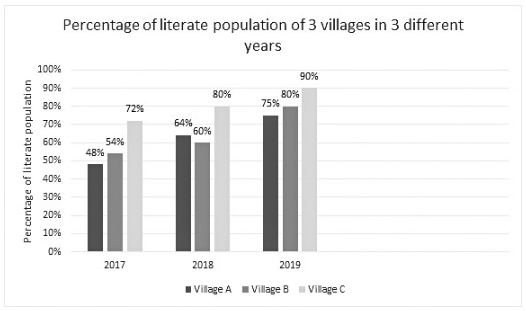
Q. If the ratio of the literate population of the three villages in the year 2016 is 2:3:5, then find the ratio of the total population of the three villages in the year 2016.
Direction: Study the given bar graph carefully and answer the questions given below.
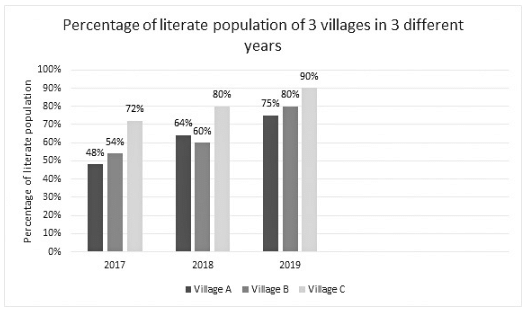
Q. If the population of the village B increased by 20% from 2016 to 2017, then by how much percentage did the literate population of the village B increased from 2016 to (2017)?
A, B, C and D are four sets such that A ∩ B = C ∩ D = ϕ. Consider the following:
1. A ∪ C and B ∪ D are always disjoint
2. A ∩ C and B ∩ D are always disjoint.
Q. Which of the above statements is/are correct?
If ![]() where P is symmetric and Q is skew symmetric matrix then P and Q are:
where P is symmetric and Q is skew symmetric matrix then P and Q are:
If I = a2 + b2 + c2, where a and b are consecutive integers and c = ab, then I is:
How many combinations are possible while selecting four letters from the word ‘SMOKEJACK’ with the condition that ‘J’ must appear in it?
If p is the length of the perpendicular from the origin on the line ![]() are in A. P. then a4 − 2p2a2 + 2p4 is equal to:
are in A. P. then a4 − 2p2a2 + 2p4 is equal to:
Let A = {x, y, z} and B = {p, q, r, s}. What is the number of distinct relations from B to A?
If 2x = 3y = 6-z, find the value of (1/x + 1/y + 1/z).
If 2(3x − 4) − 2 < 4x − 2 ≥ 2x − 4; then the possible value of x can be:
x3 + x2 + 16 is exactly divisible by x, where x is a positive integer. The number of all such possible values of x is:
A solid sphere of radius 3 cm is melted to form a right circular cone such that the height of the cone is half the radius of the cone. Find the radius of the cone.
If [x]2 − 5[x] + 6 = 0, where [.] denotes the greatest integer function, then:
What will be the percentage change in the volume of a cuboid if its length increases by 57.13%, breadth decreases by 41.66%, and height decrease by 46.66%?
The percentage of loss when an article is sold at Rs. 500 is the same as that of the profit% when it is sold at Rs. 700. Find the percentage of profit or loss on the article.
The set O of odd positive integers less than 10 can be expressed by _______.
If one of the diagonals of a square is along the line x = 2y and one of its vertices is A(3,0), then its side through this vertex is given by the equations:
There are 30 people in a group. If all shake hands with one another, how many handshakes are possible?
A man cycles at the speed of 8 km/hrs and reaches office at 11 am and when he cycles at the speed of 12 km/hrs, he reaches office at 9 am. At what speed should he cycle so that he reaches his office at 10 am?
If 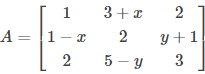 is a symmetric matrix, then 3x + y is equal to:
is a symmetric matrix, then 3x + y is equal to:
The simple and compound interest that can be earned in two years at the same rate on a certain sum is Rs. 1000 and Rs. 1040 respectively. What is the rate (percent per annum) of interest?