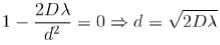OneTime: Interference NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - OneTime: Interference NAT Level - 2
A Michelson interferometer is configured as a wave meter as shown in the figure below may be used to compare the wavelengths of 2 laser with high precision when the mirror is the right arm of the interferometer is translated through a distance d, 1,00,000 interference fringes pass across the detector for green light and 85,865 fringes pass across the detector for red (λ = 632.82 nm) light. What is the wavelength of the green laser light in nm?

Light from a laser falls on a pair of very narrow slits separated by 0.5 μm & bright fringes separated by 1.0 mm are observed on a distant screen if the frequency of the laser light is doubled, how much times the separation of the bright fringes decrease(answer in integer) ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
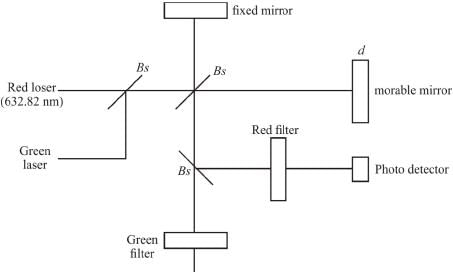
A gas filled cell of length 0.5 cm is inserted in one arm of the michelson interferometer as shown in the figure below. The interferometer is illuminated by light of wavelength 500 nm. As the gas is evaluated from the cell, 40 fringes cross a point in the field of view. Find the refractive index of this gas

Blue light of wavelength 480 nm is most strongly reflected from a thin film of oil on a glass slide when viewed near normal incidence. Assuming that the index of refraction of the oil is 1.2 & that of glass is 1.6, what is the minimum thickness of the oil film in nm (other than zero)?
In a double slit interference experiment d is the distance between the centres of the slits and w is the width of each slit. Find the minimum integer ratio d/ω for which an interference maximum of incident plane waves on a distant screen will be missing.
It is necessary to coat a glass lens with a non reflecting layer if the wavelength of the light in the coating is λ, the best choice is a layer of material having an index of refraction between those of glass & air and a thickness of what fraction of λ ?
Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?
Two coherent monochromatic light beams of intensities l and 4l are superposed. What is the minimum possible intensities in the resulting beam?
The screen of a pinhole camera is at a distance D from the pinhole. Which has a diameter d the light has an effective wavelength 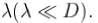 For what value of d in terms of
For what value of d in terms of 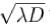 will the image be sharpest
will the image be sharpest
A student prepared a young’s double slit by drawing two parallel lines (with a separation less than a millimeter) on a smoked glass plate. Accidently, he used two different pins to draw the lines so that the widths of the slits (regions from where smoke was removed by the pin) were in the ratio 4:1. What will be the ratio of the interference maximum to that at the interference minimum?


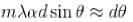 (for small angles) where d is the width of the slit & in is an integer.
(for small angles) where d is the width of the slit & in is an integer.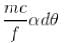
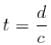 but since its speed is lower in oil,
but since its speed is lower in oil,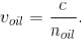
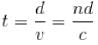
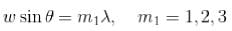
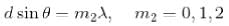
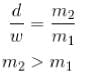
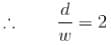
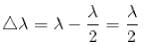
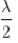
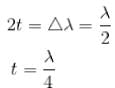
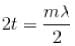
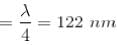
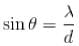
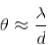
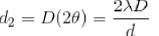
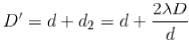 taking the first derivative, w.r.t.
taking the first derivative, w.r.t.