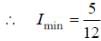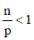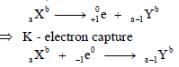JEE (Advanced) 2016 Paper - 1 with Solutions - JEE MCQ
30 Questions MCQ Test National Level Test Series for JEE Advanced 2025 - JEE (Advanced) 2016 Paper - 1 with Solutions
Inst.
Q. 1 to 5 carry 3 marks each
Each question has FOUR options (A), (B), (C) and (D). ONLY ONE of these four options is correct.
Q.
In a historical experiment to determine Planck’s constant, a metal surface was irradiated with light of different wavelengths. The emitted photoelectron energies were measured by applying a stopping potential. The relevant data for the wavelength (λ) of incident light and the corresponding stopping potential (V0) are given below:

Given that c = 3 x108 ms-1 and e = 1.6 x 10-19C, Planck’s constant (in units of J s) found from such an
experiment is
experiment is
A uniform wooden stick of mass 1.6 kg and length 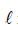 rests in an inclined manner on a smooth, vertical wall of height h (<
rests in an inclined manner on a smooth, vertical wall of height h (<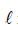 ) such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of 300 with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio h/
) such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of 300 with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio h/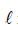 and the frictional force f at the bottom of the stick are (g = 10 ms-2)
and the frictional force f at the bottom of the stick are (g = 10 ms-2)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A water cooler of storage capacity 120 litres can cool water at a constant rate of P watts. In a closed circulation system (as shown schematically in the figure), the water from the cooler is used to cool an external device that generates constantly 3 kW of heat (thermal load). The temperature of water fed into the device cannot exceed 300C and the entire stored 120 litres of water is initially cooled to 100C. The entire system is thermally insulated. The minimum value of P (in watts) for which the device can be operated for 3 hours is
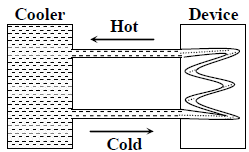
(Specific heat of water is 4.2 kJ kg-1 K-1 and the density of water is 1000 kg m-3)
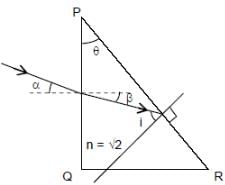
A parallel beam of light is incident from air at an angle α on the side PQ of a right angled triangular prism of refractive index n = √2. Light undergoes total internal reflection in the prism at the face PR when α has a minimum value of 450. The angle θ of the prism is
An infinite line charge of uniform electric charge density λ lies along the axis of an electrically conducting infinite cylindrical shell of radius R. At time t = 0, the space inside the cylinder is filled with a material of permittivity ε and electrical conductivity σ. The electrical conduction in the material follows Ohm’s law. Which one of the following graphs best describes the subsequent variation of the magnitude of current density j(t) at any point in the material?
Q. 6 to 13 carry 4 marks each
Each questions has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four option(s) is(are) correct.
Q. Highly excited states for hydrogen-like atoms (also called Rydberg states) with nuclear charge Ze are defined by their principal quantum number n, where n >> 1. Which of the following statement(s) is (are) true?
Two loudspeakers M and N are located 20 m apart and emit sound at frequencies 118 Hz and 121 Hz, respectively. A car is initially at a point P, 1800 m away from the midpoint Q of the line MN and moves towards Q constantly at 60 km/hr along the perpendicular bisector of MN. It crosses Q and eventually reaches a point R, 1800 m away from Q. Let v(t) represent the beat frequency measured by a person sitting in the car at time t. Let vP, vQ and vR be the beat frequencies measured at locations P, Q and R, respectively. The speed of sound in air is 330 m s-1. Which of the following statement(s) is(are) true regarding the sound
heard by the person?
An incandescent bulb has a thin filament of tungsten that is heated to high temperature by passing an electric current. The hot filament emits black-body radiation. The filament is observed to break up at random locations after a sufficiently long time of operation due to non-uniform evaporation of tungsten from the filament. If the bulb is powered at constant voltage, which of the following statement(s) is(are) true?
A plano-convex lens is made of a material of refractive index n. When a small object is placed 30 cm away
in front of the curved surface of the lens, an image of double the size of the object is produced. Due to
reflection from the convex surface of the lens, another faint image is observed at a distance of 10 cm away
from the lens. Which of the following statement(s) is(are) true?
A length-scale () depends on the permittivity (ε) of a dielectric material, Boltzmann constant (kB), the absolute temperature (T), the number per unit volume (n) of certain charged particles, and the charge (q) carried by each of the particles. Which of the following expression(s) for
is(are) dimensionally correct?
A conducting loop in the shape of a right angled isosceles triangle of height 10 cm is kept such that the 900 vertex is very close to an infinitely long conducting wire (see the figure). The wire is electrically insulated from the loop. The hypotenuse of the triangle is parallel to the wire. The current in the triangular loop is in counterclockwise direction and increased at a constant rate of 10 A s-1. Which of the following statement(s) is(are) true?
The position vector of a particle of mass m is given by the following equation
, where α = 10/3 m s-3, β= 5 m s-2 and m = 0.1 kg. At t = 1 s, which of the following statement(s) is(are) true about the particle?
A transparent slab of thickness d has a refractive index n (z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1 and n2 (> n1), as shown in the figure. A ray of light is incident with angle θi from medium 1 and emerges in medium 2 with refraction angle θf with a lateral displacement l.
Which of the following statement (s) is (are) true?
Q. 14 to 18 carry 3 marks each
The answer to each question is a SINGLE DIGIT INTEGER ranging from 0 to 9, both inclusive.
Q.
A metal is heated in a furnace where a sensor is kept above the metal surface to read the power radiated (P) by the metal. The sensor has a scale that displays log2 (P/P0), where P0 is a constant. When the metal surface is at a temperature of 487°C, the sensor shows a value 1. Assume that the emissivity of the metallic surface remains constant. What is the value displayed by the sensor when the temperature of the metal surface is raised to 2767 °C?
The isotope having a mass 12.014 u undergoes β-decay to
.
has an excited state of the nucleus at
4.041 MeV above its ground state. If
decays to
, the maximum kinetic energy of the β- particle in units of MeV is (1 u = 931.5 MeV/c2, where c is the speed of light in vacuum).
A hydrogen atom in its ground state is irradiated by light of wavelength 970 Å. Taking hc/e = 1.237×10–6 eV m and the ground state energy of hydrogen atom as –13.6 eV, the number of lines present in the emission spectrum is
Consider two solid spheres P and Q each of density 8 gm cm–3 and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density 0.8 gm cm–3 and viscosity η = 3 poiseulles. Sphere Q is dropped into a liquid of density 1.6 gm cm–3 and viscosity η = 2 poiseulles. The ratio of the terminal velocities of P and Q is
Two inductors L1 (inductance 1 mH, internal resistance 3) and L2 (inductance 2 mH, internal resistance 4
), and a resistor R (resistance 12
) are all connected in parallel across a 5V battery. The circuit is switched on at time t = 0. The ratio of the maximum to the minimum current (Imax / Imin) drawn from the battery is
Q. 19 to 23 carry 3 marks each
Each question has FOUR options (A), (B), (C) and (D). ONLY ONE of these four options is correct.
Q.
P is the probability of finding the 1s electron of hydrogen atom in a spherical shell of infinitesimal thickness, dr, at a distance r from the nucleus. The volume of this shell is 4πr2dr. The qualitative sketch of the dependence of P on r is
One mole of an ideal gas at 300 K in thermal contact with surroundings expands isothermally from 1.0 L to 2.0 L against a constant pressure of 3.0 atm. In this process, the change in entropy of surrounding (ΔSsurr)in JK–1 is (1L atm = 101.3 J)
The increasing order of atomic radii of the following Group 13 elements is
Among [Ni(CO)4], [NiCl4]2–, [Co(NH3)4Cl2]Cl, Na3[CoF6], Na2O2 and CsO2, the total number of paramagnetic compounds is
On complete hydrogenation, natural rubber produces
Q. 24 to 31 carry 4 marks each
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four option(s) is(are) correct.
Q.
According to the Arrhenius equation
A plot of the number of neutrons (N) against the number of protons (P) of stable nuclei exhibits upward deviation from linearity for atomic number, Z > 20. For an unstable nucleus having N/P ratio less than 1, the possible mode(s) of decay is(are)
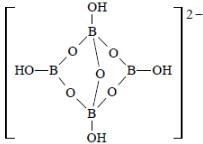
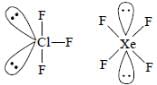
The compound(s) with TWO lone pairs of electrons on the central atom is(are)
The reagent(s) that can selectively precipitate S2– from a mixture of S2– and in aqueous solution is(are)
Positive Tollen’s test is observed for
The product(s) of the following reaction sequence is (are)
|
3 videos|3 docs|40 tests
|
|
3 videos|3 docs|40 tests
|


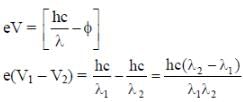
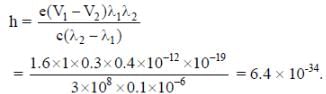
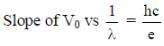
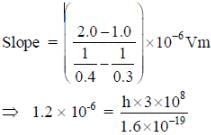
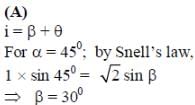
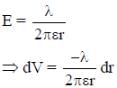
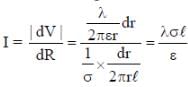
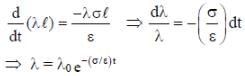
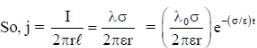
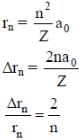
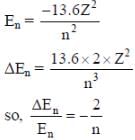
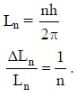
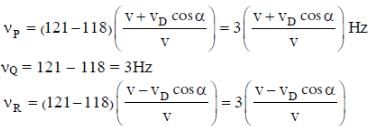
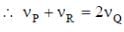
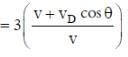
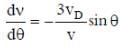
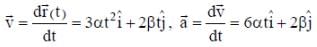
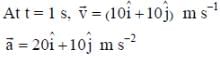
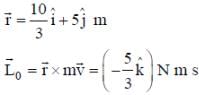
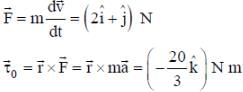
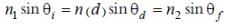
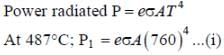
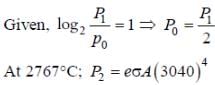
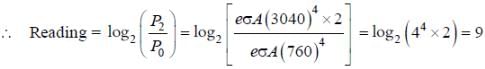
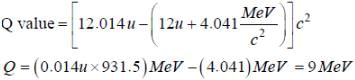
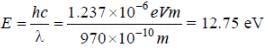 (4th energy level of hydrogen atom). Hence, the number of lines present in the emission spectrum = 4C2 = 6
(4th energy level of hydrogen atom). Hence, the number of lines present in the emission spectrum = 4C2 = 6 where ρ is the density of the solid sphere and σ is the density of the liquid
where ρ is the density of the solid sphere and σ is the density of the liquid