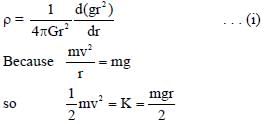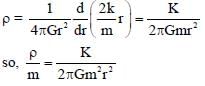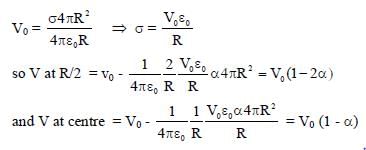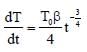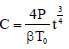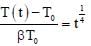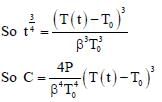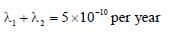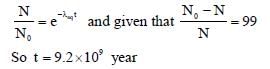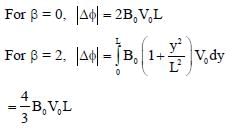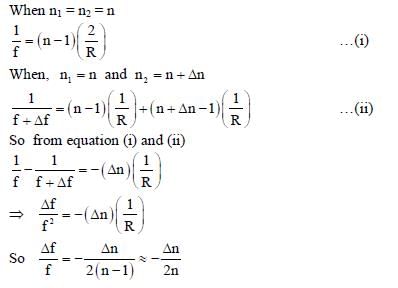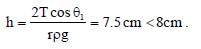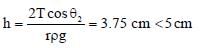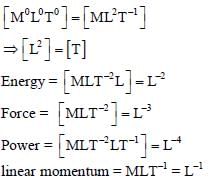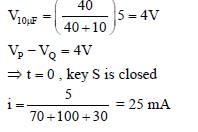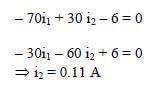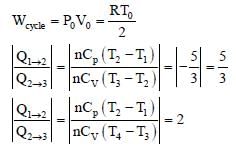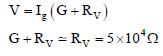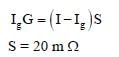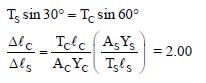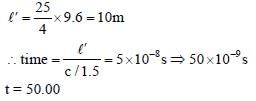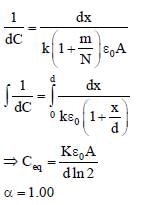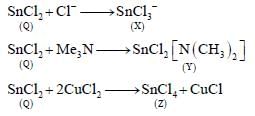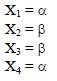JEE (Advanced) 2019 Paper - 1

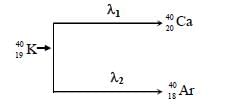
In a radioactive sample K nuclei either decay into stable Ca nuclei with decay constant 4.5x10^-10 per year or into stable 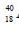 Ar nuclei with decay constant 0.5x10^-10 per year. Given that in this sample all the stable Ca and 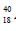 Ar nuclei are produced by the  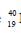K nuclei only. In time t x 10⁹ years, if the ratio of the sum of stable 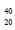Ca and  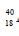Ar nuclei to the radioactive  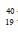K nuclei is 99, the value of t will be
[Given : ln10 = 2.3]

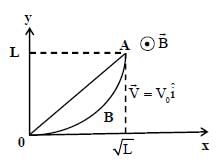
A conducting wire of parabolic shape, initially y = x², is moving with velocity 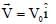 in a non uniform magnetic field  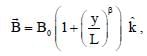as shown in figure. If V₀ , B₀, L and β are positive constants and  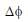is the potential difference developed between the ends of the wire, then the correct statement(s) is/are:

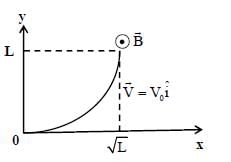
A thin convex lens is made of two materials with refractive indices n₁ and n₂, as shown in figure. The radius of curvature of the left and right spherical surfaces are equal. f is the focal length of the lens when n₁ = n₂ = n. The focal length is f + Δf when n₁ = n and n₂ = n + Δn. Assuming Δn << (n – 1) and 1 < n < 2. The correct statement(s) is/are.

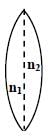
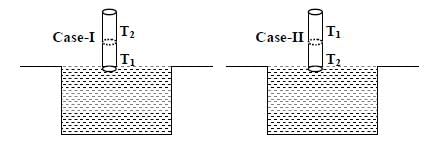
A cylindrical capillary tube of 0.2 mm radius is made by joining two capillaries T₁ and T₂ of different materials having water contact angles of 0⁰ and 60⁰, respectively. The capillary tube is dipped vertically in water in two different configurations, case I and II as shown in figure. Which of the following option(s) is (are) correct?
[Surface tension of a water = 0.075 N/m, density of water = 1000 kg/m³, take g = 10 m/s²]

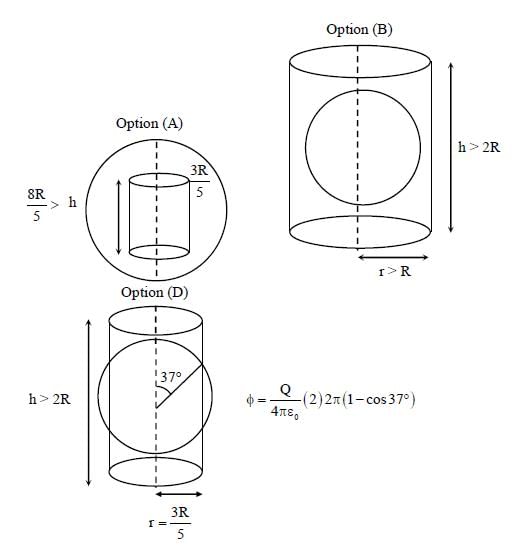
A charged shell of radius R carries a total charge Q. Given 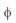 as the flux of electric field through a closed cylindrical surface of height h, radius r and with its center same as that of the shell. Here, center of thecylinder is a point on the axis of the cylinder which is equidistant from its top and bottom surfaces. Whichof the following option(s) is/are correct?
[ε₀ is permittivity of free space]

Let us consider a system of units in which mass and angular momentum are dimensionless. If length hasdimension of L, which of the following statement(s) is/are correct?

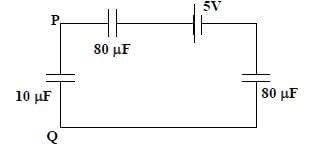
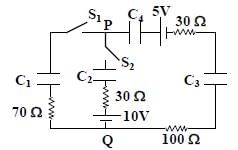
In the circuit shown, initially there is no charge on capacitors and keys S₁ and S₂ are open. The values of the capacitors are 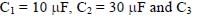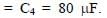Which of the statement(s) is/are correct?

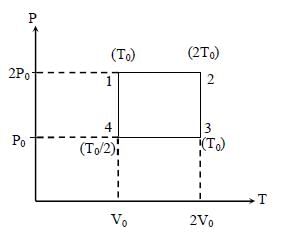
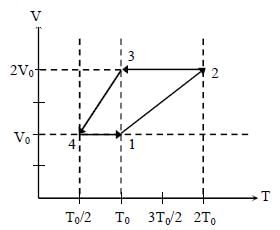
One mole of a monatomic ideal gas goes through athermodynamic cycle, as shown in the volume versustemperature (V – T) diagram. The correct statement(s) is/are:[R is the gas constant]

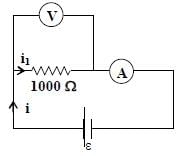
Two identical moving coil galvanometers have 10 Ω resistance and full scale deflection at 2 μA current.One of them is converted into a voltmeter of 100 mV full scale reading and the other into an Ammeter of1mA full scale current using appropriate resistors. These are then used to measure the voltage and currentin the Ohm’s law experiment with R = 1000 Ω resistor by using an ideal cell. Which of the followingstatement(s) is/are correct?

A block of weight 100 N is suspended by copper andsteel wires of same cross sectional area 0.5 cm² and,length 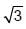m and 1 m, respectively. Their otherends are fixed on a ceiling as shown in figure. Theangles subtended by copper and steel wires withceiling are 30° and 60°, respectively. If elongation incopper wire is 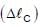and elongation in steel wire is 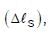then the ratio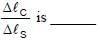
[Young’s modulus for copper and steel are 1 × 10¹¹ N/m² and 2 × 10¹¹ N/m², respectively.]

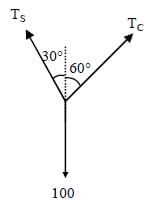
A particle is moved along a path AB-BC-CD-DE-EF-FA, as shown in figure,

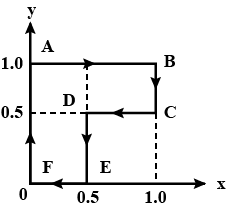
in presence of a force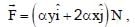where x and y are in meter and 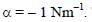The work done on the particle by this force 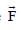will be _______ Joule.

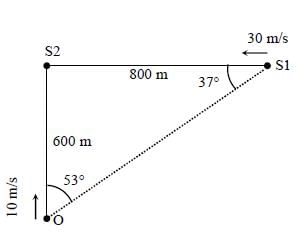
A train S1, moving with a uniform velocity of 108 km/h, approaches another train S2 standing on a platform. An observer O moves with a uniform velocity of 36 km/h towards S2, as shown in figure. Both the trains are blowing whistles of same frequency 120 Hz. When O is 600 m away from S2 and distance between S1 and S2 is 800 m, the number of beats heard by O is _____________
.[Speed of the sound = 330 m/s]

A liquid at 30°C is poured very slowly into a Calorimeter that is at temperature of 110°C. The boiling temperature of the liquid is 80°C. It is found that the first 5 gm of the liquid completely evaporates. After pouring another 80 gm of the liquid the equilibrium temperature is found to be 50°C. The ratio of the Latent heat of the liquid to its specific heat will be _____________°C.[Neglect the heat exchange with surrounding]

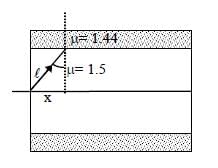
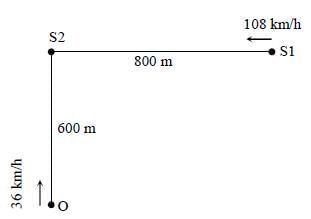
A planar structure of length L and width W is made of two different optical media of refractive indices n₁ = 1.5 and n₂ = 1.44 as shown in figure. If L >> W, a ray entering from end AB will emerge from end CD only if the total internal reflection condition is met inside the structure. For L = 9.6 m, if the incident angle θ is varied, the maximum time taken by a ray to exit the plane CD is t × 10^–9 s, where t is ________.
[Speed of light c = 3 × 10⁸ m/s]

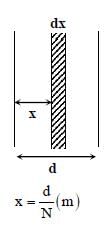
A parallel plate capacitor of capacitance C has spacing d between two plates having area A. The region between the plates is filled with N dielectric layers, parallel to its plates, each with thickness 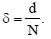The dielectric constant of the 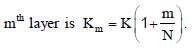For a very large 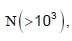the capacitance C is 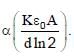The value of α will be ___________.
[∈₀ is the permittivity of free space]

The green colour produced in the borax bead test of a chromium(III) salt is due to

Molar conductivity (∧_m) of aqueous solution of sodium stearate, which behaves as a strong electrolyte, isrecorded at varying concentrations (c) of sodium stearate. Which one of the following plots provides thecorrect representation of micelle formation in the solution?
(critical micelle concentration (CMC) is marked with an arrow in the figures

Calamine, malachite, magnetite and cryolite, respectively, are

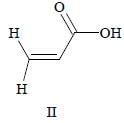
The correct order of acid strength of the following carboxylic acids is

Which of the following statements(s) is (are) true ?

Choose the correct option(s) for the following set of reactions

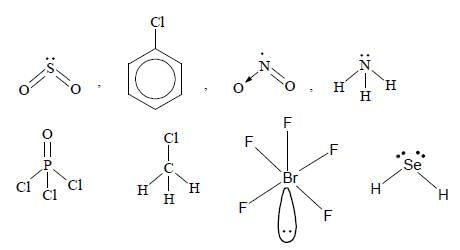
Each of the following options contains a set of four molecules, Identify the option(s) where all four molecules possess permanent dipole moment at room temperature.

Choose the reaction(s) from the following options, for which the standard enthalpy of reaction is equal to the standard enthalpy of formation.

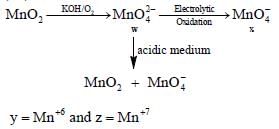
Fusion of MnO₂ with KOH in presence of O₂ produces a salt W. Alkaline solution of W upon electrolyticoxidation yields another salt X. The manganese containing ions present in W and X, respectively, are Y andZ. Correct statement(s) is(are)

Which of the following statement(s) is(are) correct regarding the root mean square speed 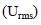and average translational kinetic energy 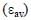of a molecule in a gas at equilibrium ?

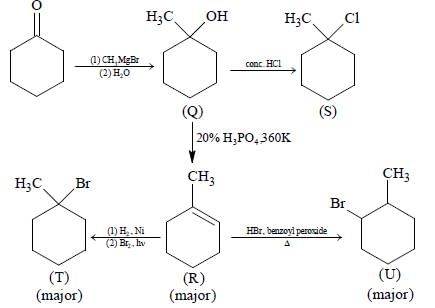
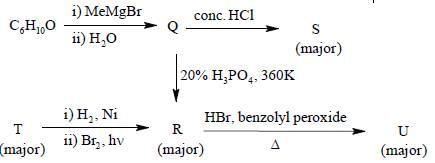
A tin chloride Q undergoes the following reactions (not balanced)

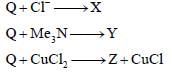
X is a monoanion having pyramidal geometry. Both Y and Z are neutral compounds. Choose the correct
option(s)

In the decay sequence,

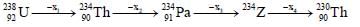
x₁, x₂, x₃ and x₄ are particles /radiation emitted by the respective isotopes. The correct option(s) is(are)

Among B₂H₆, B₃N₃H₆, N₂O, N₂O₄, H₂S₂O₃ and H₂S₂O₈, the total number of molecules containing covalent bond between two atoms of the same kind is

On dissolving 0.5 g of a non-volatile non-ionic solute to 39 g of benzene, its vapour pressure decreases
from 650 mm Hg to 640 mm Hg. The depression of freezing point of benzene (in K) upon addition of the
solute is
(Given data: Molar mass and the molal freezing point depression constant of benzene are 78 g mol^-1 and 5.12 K kg mol^–1, respectively)

For the following reaction, the equilibrium constant

When equal volumes of 0.06 M Fe²⁺(aq) and 0.2 M S^2–(aq) solutions are mixed, the equilibrium concentration of Fe²⁺(aq) is found to be Y x 10^–17 M. The value of Y is ……… .

The rate of the reaction for [A] = 0.15 mol dm^–3, [B] = 0.25 mol dm^–3 and [C] = 0.15 mol dm^–3 is found to be Y x 10^–5 mol dm^–3s^–1. The value of Y is ………..

Schemes 1 and 2 describe the conversion of P to Q and R to S, respectively. Scheme 3 describes the synthesis of T from Q and S. The total number of Br atoms in a molecule of T is

At 143 K, the reaction of XeF₄ with O₂F₂ produces xenon compound Y. The total number of lone Pair(s) of electrons present on the whole molecule of Y is ………

are real numbers, and 1 is the
2 x 2 identity matrix. If α* is the minimum of the set is the minimum of the set then the value of

The area of the region

Let S be the set of all complex numbers z satisfying If the complex number z₀ is such that is the maximum of the set then the principal argument of

A line y = mx + 1 intersects the circle (x – 3)² + (y + 2)² = 25 at the points P and Q. If the midpoint of the
line segment PQ has x-coordinate then which one of the following options is correct?

Let  α and  β be the roots of x² – x – 1= 0, with α > β. For all positive integers n, define Then which of the following options is/are correct?

In a non-right-angled triangle ΔPQR, let p, q, r denote the lengths of the sides opposite to the angles at P, Q, R respectively. The median from R meets the side PQ at S, the perpendicular from P meets the side QR at E, and RS and PE intersect at O. If  , q = 1, and the radius of the circumcircle of the ΔPQR equals 1, then which of the following options is/are correct?

Let  denote a curve y = y(x) which is in the first quadrant and let the point (1, 0) lie on it. Let the tangent to  at a point P intersect the y-axis at Y_P. If PY_P has length l for each point P on , then which of the following option is/are correct?

where a and b area real numbers. Which of the following options is/are correct?

Define the collections {E₁, E₂, E₃, …….} of ellipses and {R₁, R₂, R₃, …} of rectangles as follows:

R₁ : rectangle of largest area, with sides parallel to the axes, inscribed in E₁;

R_n: rectangle of largest area, with sides parallel to the axes, inscribed in E_n, n > 1. Then which of the following options is/are correct?

Then which of the following options is/are correct?

Let L₁ and L₂ denote the lines and respectively. If L₃ is a line which is perpendicular to both L₁ and L₂ and cuts both of them, then which of the following options describe (s) L₃?

There are three bags B₁, B₂ and B₃. The bag B₁ contains 5 red and 5 green balls, B₂ contains 3 red and 5
green balls and B₃ contains 5 red and 3 green balls. Bags B₁, B₂ and B₃ have probabilities respectively of being chosen. A bag is selected at random and a ball is chosen at random from the bag. Then which of the following options is/are correct?

be a cube root of unity. Then the minimum of the set : a, b, c distinct non–zero integers} equals _____

Let S be the sample space of all 3 x 3 matrices with entries from the set {0, 1}. Let the events E₁ and E₂ be given by
E1 = {A ∈ S : det A = 0} and
E2 ={A ∈ S : sum of entries of A is 7}
If a matrix is chosen at random from S, then the conditional probability P(E1/E2) equals _____

Let the point B be the reflection of the point A(2, 3) with respect to line 8x – 6y – 23 = 0. Let  be circles of radii 2 and 1 with centres A and B respectively. Let T be a common tangent to the circles  and  such that both the circles are on the same side of T. If C is the point of intersection of T and the line passing through A and B, then the length of the line segment AC is _____

Let AP(a; d) denote the set of all the terms of an infinite arithmetic progression with first term a and common difference

Three lines are given by Let the lines cut the plane x + y + z = 1 at the points A, B and C respectively. If the area of the triangle ABC is Δ then the value of equals