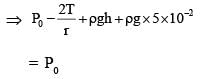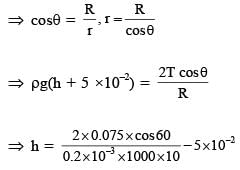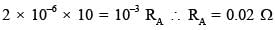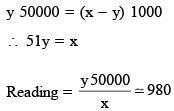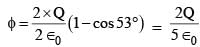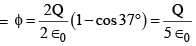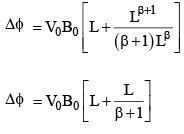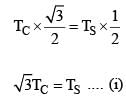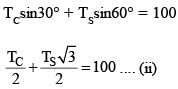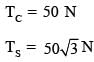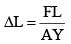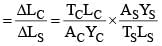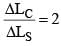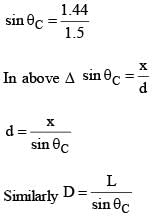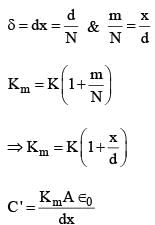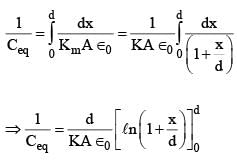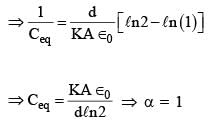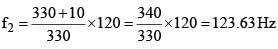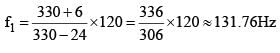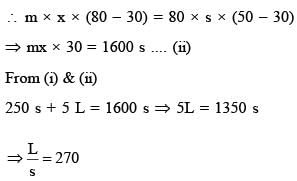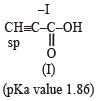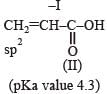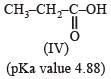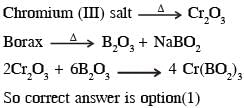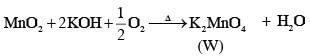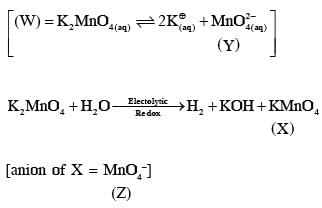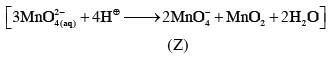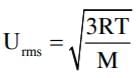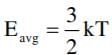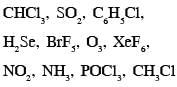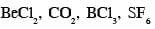JEE Advanced 2019 Question Paper with Solutions (27th May - Morning) - JEE MCQ
30 Questions MCQ Test - JEE Advanced 2019 Question Paper with Solutions (27th May - Morning)
A current carrying wire heats a metal rod. The wire provides a constant power (P) to the rod. The metal rod is enclosed in an insulated container. It is observed that the temperature (T) in the metal rod changes with time (t) as:
T(t) = T0 (1 + βt1/4)
where β is a constant with appropriate dimension while T0 is a constant with dimension of temperature. The heat capacity of the metal is:
T(t) = T0 (1 + βt1/4)
where β is a constant with appropriate dimension while T0 is a constant with dimension of temperature. The heat capacity of the metal is:
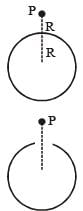
A thin spherical insulating shell of radius R carries a uniformly distributed charge such that the potential at its surface is V0. A hole with a small area α4πR2 (α<<1) is made on the shell without affecting the rest of the shell. Which one of the following statements is correct?
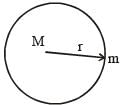
Consider a spherical gaseous cloud of mass density ρ(r) in free space where r is the radial distance from its center. The gaseous cloud is made of particles of equal mass m moving in circular orbits about the common center with the same kinetic energy K. The force acting on the particles is their mutual gravitational force. If ρ(r) is constant in time, the particle number density n(r) = ρ(r)/m is :
[G is universal gravitational constant]
[G is universal gravitational constant]
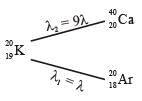
In a radioactive sample, 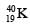 nuclei either decay into stable
nuclei either decay into stable 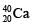 nuclei with decay constant 4.5 × 10–10 per year or into stable
nuclei with decay constant 4.5 × 10–10 per year or into stable 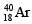 nuclei with decay constant 0.5 × 10–10 per year. Given that in this sample all the stable
nuclei with decay constant 0.5 × 10–10 per year. Given that in this sample all the stable 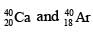 nuclei are produced by the
nuclei are produced by the 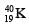 nuclei only. In time t × 109 years, if the ratio of the sum of stable
nuclei only. In time t × 109 years, if the ratio of the sum of stable 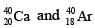 nuclei to the radioactive
nuclei to the radioactive 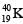 nuclei is 99, the value of t will be: [Given ln 10 = 2.3]
nuclei is 99, the value of t will be: [Given ln 10 = 2.3]
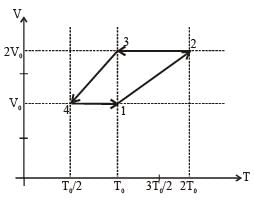
One mole of a monoatomic ideal gas goes through a thermodynamic cycle, as shown in the volume versus temperature (V - T) diagram. The correct statement(s) is/are:
[R is the gas constant]
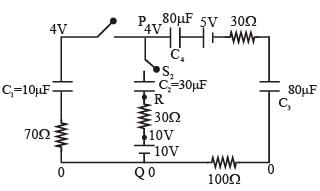
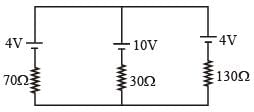
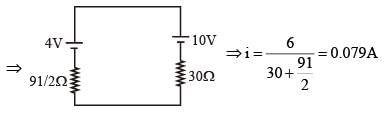
In the circuit shown, initially, there is no charge on capacitors and keys S1 and S2 are open. The values of the capacitors are C1 = 10 μF, C2 = 30 μF and C3 = C4 = 80 μF.
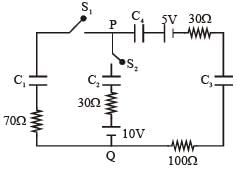
Which of the statement(s) is/are correct?
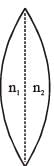
A thin convex lens is made of two materials with refractive indices n1 and n2, as shown in figure. The radius of curvature of the left and right spherical surfaces are equal. f is the focal length of the lens when n1 = n2 = n. The focal length is f + Δf when n1 = n and n2 = n + Δn. Assuming Δn << (n–1) and 1 < n < 2, the correct statement(s) is/are:
Let us consider a system of units in which mass and angular momentum are dimensionless. If length has dimension of L, which of the following statement (s) is/are correct?
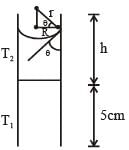
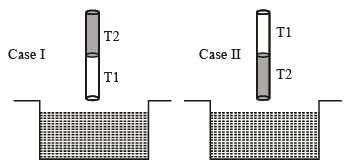
A cylindrical capillary tube of 0.2 mm radius is made by joining two capillaries T1 and T2 of different materials having water contact angles of 0° and 60°, respectively. The capillary tube is dipped vertically in water in two different configurations, case I and II as shown in figure. Which of the following option(s) is(are) correct?
(Surface tension of water = 0.075 N/m, density of water = 1000 kg/m3, take g = 10 m/s2)
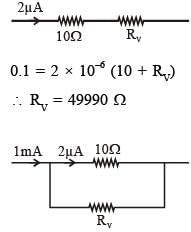
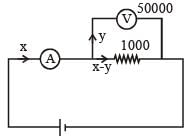
Two identical moving coil galvanometer have 10 Ω resistance and full scale deflection at 2 µA current. One of them is converted into a voltmeter of 100 mV full scale reading and the other into an Ammeter of 1 mA full scale current using appropriate resistors. These are then used to measure the voltage and current in the Ohm's law experiment with R = 1000 Ω resistor by using an ideal cell. Which of the following statement(s) is/are correct?
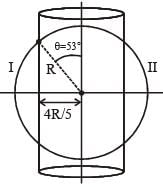
A charged shell of radius R carries a total charge Q. Given φ as the flux of electric field through a closed cylindrical surface of height h, radius r and with its center same as that of the shell. Here, center of the cylinder is a point on the axis of the cylinder which is equidistant from its top and bottom surfaces. Which of the following option(s) is/are correct ? [∈0 is the permittivity of free space]
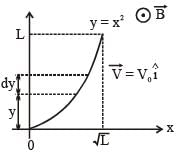
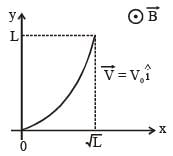
A conducting wire of parabolic shape, initially y = x2, is moving with velocity  in a non-uniform magnetic field
in a non-uniform magnetic field 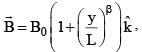 as shown in figure. If V0, B0, L and β are positive constants and Δφ is the potential difference developed between the ends of the wire, then the correct statement(s) is/are:
as shown in figure. If V0, B0, L and β are positive constants and Δφ is the potential difference developed between the ends of the wire, then the correct statement(s) is/are:
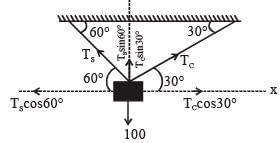
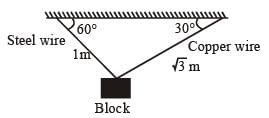
A block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5 cm2 and, length √3 m and 1 m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30° and 60°, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio 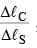 is _____.
is _____.
[Young's modulus for copper and steel are 1 × 1011 N/m2 and 2 × 1011 N/m2 respectively]
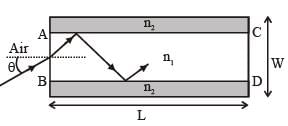
A planar structure of length L and width W is made of two different optical media of refractive indices n1 = 1.5 and n2 = 1.44 as shown in figure. If L >> W, a ray entering from end AB will emerge from end CD only if the total internal reflection condition is met inside the structure. For L = 9.6 m, if the incident angle θ is varied, the maximum time taken by a ray to exit the plane CD is t × 10–9 s, where t is ____. [Speed of light c = 3 × 108 m/s]
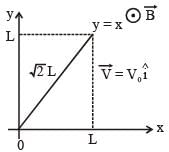
A particle is moved along a path AB-BC-CD-DE-EF-FA, as shown in figure, in presence of a force 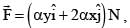 where x and y are in meter and α = –1 N/m–1. The work done on the particle by this force
where x and y are in meter and α = –1 N/m–1. The work done on the particle by this force 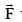 will be ____ Joule.
will be ____ Joule.

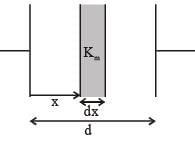
A parallel plate capacitor of capacitance C has spacing d between two plates having area A. The region between the plates is filled with N dielectric layers, parallel to its plates, each with thickness δ = d/N. The dielectric constant of the mth layer is 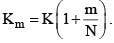 For a very large N (> 103), the capacitance C is
For a very large N (> 103), the capacitance C is 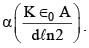 The value of α will be _____.
The value of α will be _____.
[∈0 is the permittivity of free space]
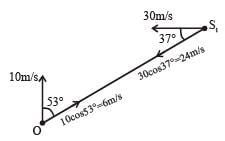
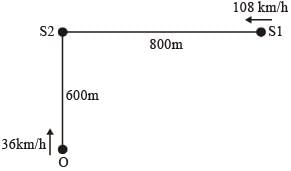
A train S1, moving with a uniform velocity of 108 km/h, approaches another train S2 standing on a platform.
An observer O moves with a uniform velocity of 36 km/h towards S2, as shown in figure. Both the trains are blowing whistles of same frequency 120 Hz. When O is 600 m away from S2 and distance between S1 and S2 is 800 m, the number of beats heard by O is ____.
[Speed of the sound = 330 m/s]
A liquid at 30°C is poured very slowly into a Calorimeter that is at temperature of 110°C. The boiling temperature of the liquid is 80°C. It is found that the first 5 gm of the liquid completely evaporates. After pouring another 80 gm of the liquid the equilibrium temperature is found to be 50°C. The ratio of the Latent heat of the liquid to its specific heat will be ______ °C.
[Neglect the heat exchange with surrounding]
Molar conductivity (∧m) of aqueous solution of sodium stearate, which behaves as a strong electrolyte, is recorded at varying concentrations (c) of sodium stearate. Which one of the following plots provides the correct representation of micelle formation in the solution?
(Critical micelle concentration (CMC) is marked with an arrow in the figures.)
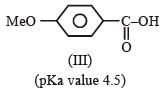
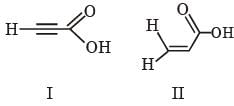
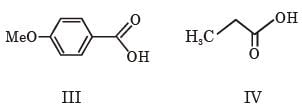
The correct order of acid strength of the following carboxylic acids is -
Calamine, malachite, magnetite and cryolite, respectively are
The green colour produced in the borax bead test of a chromium(III) salt is due to -
Fusion of MnO2 with KOH in presence of O2 produces a salt W. Alkaline solution of W upon electrolytic oxidation yields another salt X. The manganese containing ions present in W and X, respectively, are Y and Z. Correct statement(s) is (are)
Which of the following statement(s) is (are) correct regarding the root mean square speed (Urms) and average translational kinetic energy (εav) of a molecule in a gas at equilibrium?
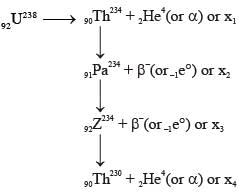
In the decay sequence:
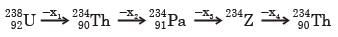
x1, x2, x3 and x4 are particles/ radiation emitted by the respective isotopes. The correct option(s) is/are
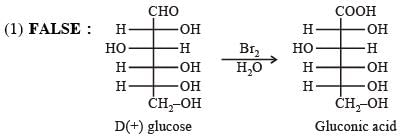
Which of the following statement(s) is(are) true?
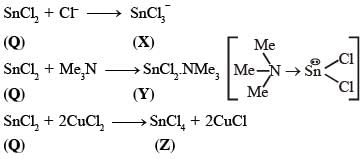
A tin chloride Q undergoes the following reactions (not balanced)
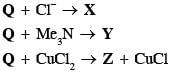
X is a monoanion having pyramidal geometry. Both Y and Z are neutral compounds. Choose the correct option(s).
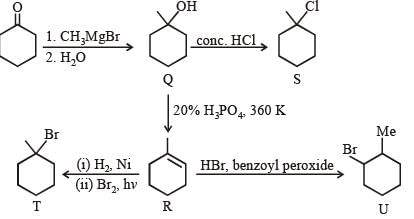
Choose the correct option(s) for the following set of reactions
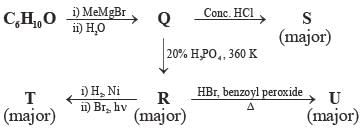
Each of the following options contains a set of four molecules. Identify the option(s) where all four molecules possess permanent dipole moment at room temperature.
Choose the reaction(s) from the following options, for which the standard enthalpy of reaction is equal to the standard enthalpy of formation.


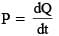
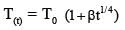
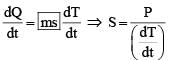
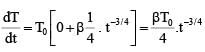
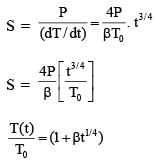
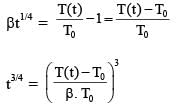

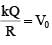
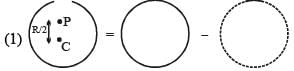
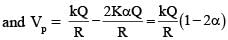
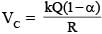

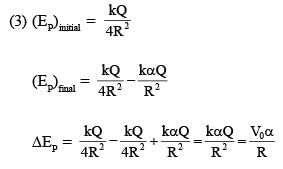
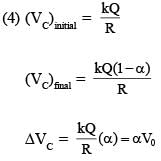

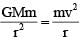
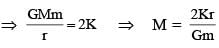
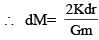
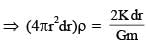
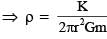

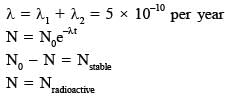
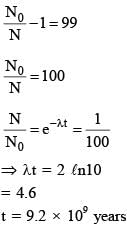

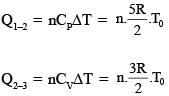
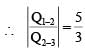

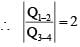
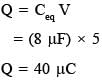
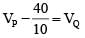
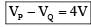
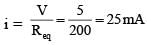
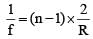
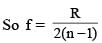 ...(1)
...(1)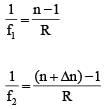
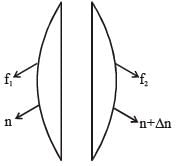
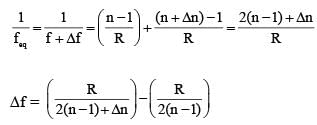

 ...(2)
...(2)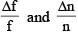 is independent of R so (1) is correct.
is independent of R so (1) is correct.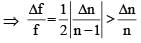
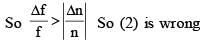
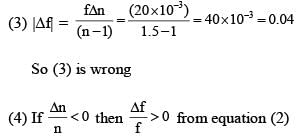
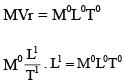

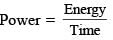

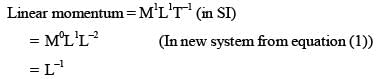
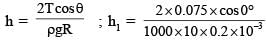
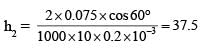 mm (in T2) [If we assume entire tube of T2]
mm (in T2) [If we assume entire tube of T2]