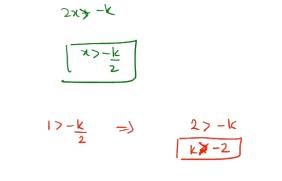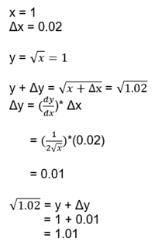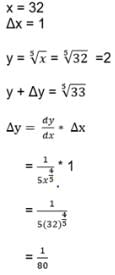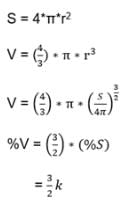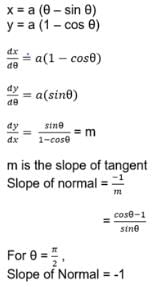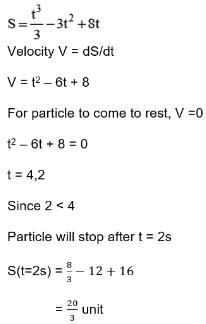JEE Advanced Level Test: Application of Derivative- 2 - EmSAT Achieve MCQ
30 Questions MCQ Test Mathematics for EmSAT Achieve - JEE Advanced Level Test: Application of Derivative- 2
The value of ‘a’ for which x3 - 3x + a = 0 has two distinct roots in [0, 1] is given by
The value of ‘c’ in Lagrange’s mean value theorem for f (x) = x (x- 2)2 in [0, 1]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
For the function f (x) = x3 - 6x2 + ax + b, if Roll’s theorem holds in [1, 3] with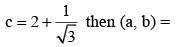 
Find Value of ‘c’ by using Rolle’s theorem for f (x) = log (x2 + 2) - log 3 on [-1,1]
The chord joining the points where x = p and x = q on the curve y = ax2 + bx + c is parallel to the tangent at the point on the curve whose abscissa is
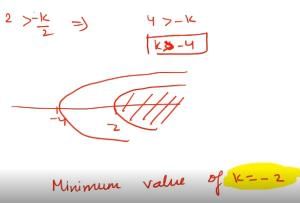
The least value of k for which the function f(x) = x2 + kx + 1 is a increasing function in the interval 1 < x < 2
The interval in which f (x) = x3 - 3x2 - 9x + 20 is strictly decreasing
The number of stationary points of f (x) = sin x in [0,2π] are
Therefore number of stationary points of f (x) in [0, 2π] is 2.Local minimum values of the function 
If the function 
has maximum at x =-3, then the value of ‘a’ is
since f (x) has local maximum at x = -3 ⇒ f ' (-3) = 0 and f 11 (-3)< 0
The point at which f (x) = (x- 1)4 assumes local maximum or local minimum value are
The global maximum and global minimum of f (x) = 2x3 - 9x2 + 12x + 6 in [0, 2]
If the percentage error in the surface area of sphere is k, then the percentage error in its volume is
If an error of 
is made in measuring the radius of a sphere then percentage error in its volume is
The height of a cylinder is equal to its radius. If an error of 1 % is made in its height. Then the percentage error in its volume is
The slope of the normal to the curve given by 
The line 
is a tangent to the curve 
then n ∈
The points on the curve 
at which the tangent is perpendicular to x-axis are
The point on the curve 
at which the tangent drawn is 
The sum of the squares of the intercepts on the axes of the tangent at any point on the curve x 2/3 + y2/3= a2/3 is
If the straight line x cos α + y sinα = p touches the curve 
at the point (a, b) on it, then
If the curves x = y² and xy = k cut each other orthogonally then k² =
The angle between the curves y = x³ and 
If the curves ay + x² = 7 and x³ = y cut orthogonally at (1, 1) then a =
Slope of the second curve at (1, 1) is m2 = 3 
A particle moves along a line is given by
then the distance travelled by the particle before it first comes to rest is
A particle is moving along a line such that s = 3t3 - 8t + 1. Find the time ‘t’ when the distance ‘S’ travelled by the particle increases.
A particle moves along a line by S = t3 - 9t2 + 24t the time when its velocity decreases.
|
141 videos|213 docs|254 tests
|
|
141 videos|213 docs|254 tests
|
Top Courses for EmSAT Achieve
Important Questions for JEE Advanced Level Test: Application of Derivative- 2
JEE Advanced Level Test: Application of Derivative- 2 MCQs with Answers
Online Tests for JEE Advanced Level Test: Application of Derivative- 2 Mathematics for EmSAT Achieve
|
© EduRev
|
Education Revolution
|
|
