JEE Advanced Level Test: Inverse Trigonometry- 3 - Airforce X Y / Indian Navy SSR MCQ
20 Questions MCQ Test - JEE Advanced Level Test: Inverse Trigonometry- 3
The set of values of ‘a’ for which x2 + ax + sin–1 (x2 – 4x + 5) + cos–1 (x2 – 4x+5 ) = 0 has at least one solution is
The value of x for which sin [cot–1(1+x)] = cos(tan–1x)
The value of 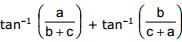 , if ∠C = 900 in triangle ABC, is
, if ∠C = 900 in triangle ABC, is
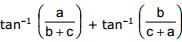 , if ∠C = 900 in triangle ABC, is
, if ∠C = 900 in triangle ABC, is The complete solution set of the inequality [cot–1 x]2 – 6[cot–1 x] + 9 ≤0 is (where [ * ] denotes the greatest integer function)
The number of solution(s) of the equation, sin–1x + cos–1 (1 – x) = sin–1 (– x), is/are
If sin-1 x + sin-1 y + sin-1z = 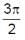 , then
, then
If α satisfies the inequation x2 – x – 2 > 0, then which of the following exists
If the numerical value of tan (cos–1 (4/5) + tan–1 (2/3)) is a/b then
Let f(x) = sin–1 x + cos–1 x. Then π/2 is equal to
α, β and γ are three angles given by 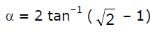 ,
,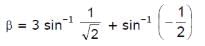 and γ = cos-1 1/3. then
and γ = cos-1 1/3. then
For the equation 2x = tan (2 tan–1 a) + 2 tan (tan–1 a + tan–1 a3), which of the following is invalid ?


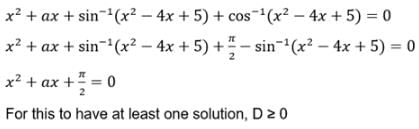
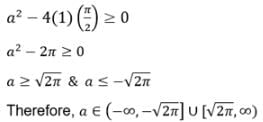

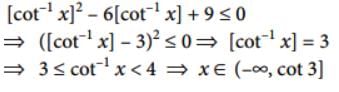

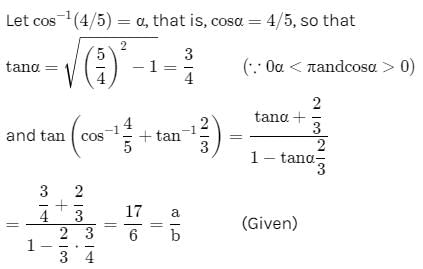
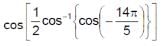 is
is 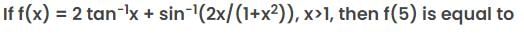
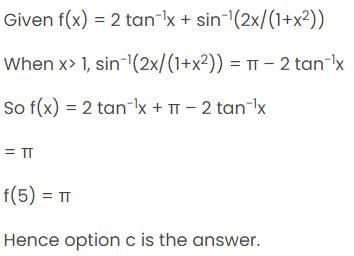


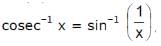 , then x may be
, then x may be 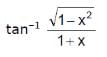 is equal to
is equal to 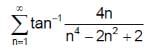 is equal to
is equal to 










