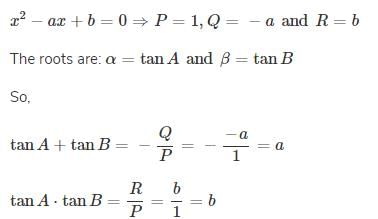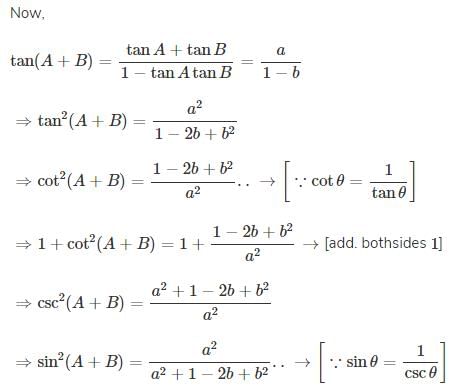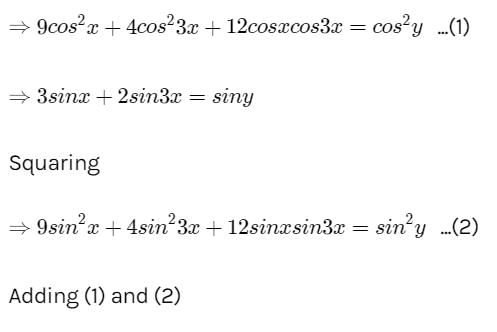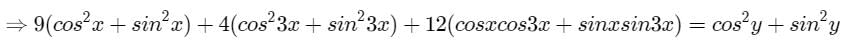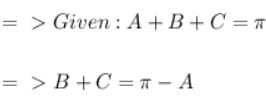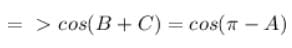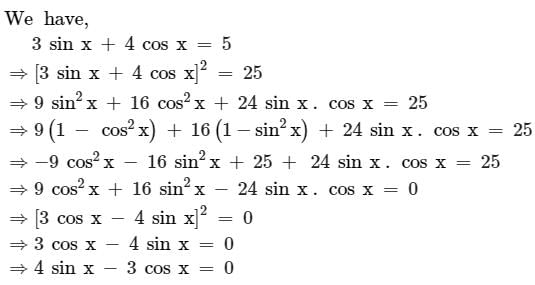JEE Advanced Level Test: Trigonometric Ratio- 2 - NDA MCQ
25 Questions MCQ Test Mathematics for NDA - JEE Advanced Level Test: Trigonometric Ratio- 2
If tan A and tan B are the roots of the quadratic equation x2 – ax + b = 0, then the value of sin2 (A + B)
If A = tan 6º tan 42º and B = cot 66º cot 78º, then
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If A + B + C = p & sin = k sin C/2,then tan A/2 tan B/2 =
In any triangle ABC, which is not right angled S cos A . cosec B . cosec C is equal to
If 3 cos x + 2 cos 3x = cos y, 3 sin x + 2 sin 3x = sin y, then the value of cos 2x is
If cos a + cos b = a, sin a + sin b = b and a - b = 2q, then =
If A + B + C = p & cos A = cos B . cos C then tan B . tanC has the value equal to
The value of tan + 2 tan π/8 + 4 is equal to
The value of cos π/19 +cos+cos+...+ cos 17π/19 is equal to
Consider a right angle triangle PQR, if PQ is 27 and QR is 17 then the value of angle P is
If f(q) = sin4 q + cos2 q, then range of f(q) is
If 2 cos x + sin x = 1, then value of 7 cos x + 6 sin x is equal to
If cosec A + cot A = 11/2, then tan A is
If 0° < x < 90° & cos x = 3/√10, then the value of log10 sin x + log10 cos x + log10 tan x is
If cot a + tan a = m and 1/cos α – cos a = n, then
If 2 sec2 a – sec4 a – 2 cosec2 a + cosec4 a = 15/4, then tan a is equal to
If , 0 < A, B < π/2, then tan A + tan B is equal to
If 3 sin x + 4 cos x = 5 then 4 sin x – 3 cos x is equal to
If sin 2q = k, then the value of is equal to
If f(q) = sin2 q + sin2 + sin2
, then f
is equal to
If (sec A + tan A) (sec B + tan B) (sec C + tan C) = (sec A – tan A) (sec B – tan B) (sec C – tan C) then each side is equal to
If tan2 q = 2 tan2 f + 1, then the value of cos 2q + sin2 f is
|
277 videos|265 docs|221 tests
|