JEE Main 2020 Question Paper with Solution (27th September - Evening) - JEE MCQ
30 Questions MCQ Test Additional Study Material for JEE - JEE Main 2020 Question Paper with Solution (27th September - Evening)
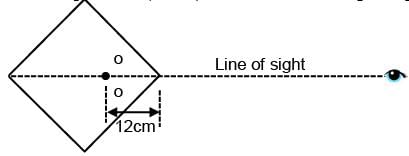
A large square container with thin transparent vertical walls and filled with water (refractive index 4/3 ) is kept on a horizontal table. A student holds a thin straight wire vertically inside the water 12 cm from one of its corners, as shown schematically in the figure. Looking at the wire from this corner, another student sees two images of the wire, located symmetrically on each side of the line of sight as shown. The separation (in cm) between these images is ____________.

A train with cross-sectional area St is moving with speed vt inside a long tunnel of cross-sectional area S0(S0=4St). Assume that almost all the air (density ρ) in front of the train flows back between its side and the walls of the tunnel. Also, the air flow with respect to the train is steady and laminar. Take the ambient pressure and that inside the train to be p0. If the pressure in the region between the sides of the train and the tunnel walls is p, then p0−p=  The value of N is ________.
The value of N is ________.
 The value of N is ________.
The value of N is ________.| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
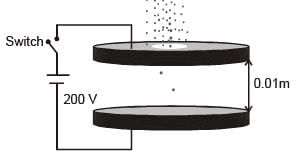
Two large circular discs separated by a distance of 0.01 m are connected to a battery via a switch as shown in the figure. Charged oil drops of density 900 kg m−3 are released through a tiny hole at the center of the top disc. Once some oil drops achieve terminal velocity, the switch is closed to apply a voltage of 200 V across the discs. As a result, an oil drop of radius 8×10−7 m stops moving vertically and floats between the discs. The number of electrons present in this oil drop is ________. (neglect the buoyancy force, take acceleration due to gravity =10 ms−2 and charge on an electron (e) = 1.6 ×10–19 C)

A hot air balloon is carrying some passengers, and a few sandbags of mass 1 kg each so that its total mass is 480 kg. Its effective volume giving the balloon its buoyancy is V. The balloon is floating at an equilibrium height of 100 m. When N number of sandbags are thrown out, the balloon rises to a new equilibrium height close to 150 m with its volume V remaining unchanged. If the variation of the density of air with height h from the ground is 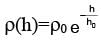 , where ρ0=1.25 kg m−3 and h0=6000 m, the value of N is _____.
, where ρ0=1.25 kg m−3 and h0=6000 m, the value of N is _____.
A point charge q of mass m is suspended vertically by a string of length l. A point dipole of dipole moment 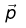 is now brought towards q from infinity so that the charge moves away. The final equilibrium position of the system including the direction of the dipole, the angles and distances is shown in the figure below. If the work done in bringing the dipole to this position is N×(mgh), where g is the acceleration due to gravity, then the value of N is _________ . (Note that for three coplanar forces keeping a point mass in equilibrium,
is now brought towards q from infinity so that the charge moves away. The final equilibrium position of the system including the direction of the dipole, the angles and distances is shown in the figure below. If the work done in bringing the dipole to this position is N×(mgh), where g is the acceleration due to gravity, then the value of N is _________ . (Note that for three coplanar forces keeping a point mass in equilibrium, 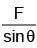 is the same for all forces, where F is any one of the forces and θ is the angle between the other two forces)
is the same for all forces, where F is any one of the forces and θ is the angle between the other two forces)
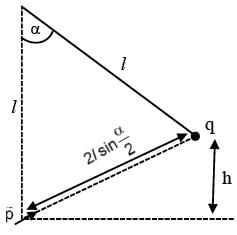
A thermally isolated cylindrical closed vessel of height 8 m is kept vertically. It is divided into two equal parts by a diathermic (perfect thermal conductor) frictionless partition of mass 8.3 kg. Thus the partition is held initially at a distance of 4 m from the top, as shown in the schematic figure below. Each of the two parts of the vessel contains 0.1 mole of an ideal gas at temperature 300 K. The partition is now released and moves without any gas leaking from one part of the vessel to the other. When equilibrium is reached, the distance of the partition from the top (in m) will be _______ (take the acceleration due to gravity =10 ms−2 and the universal gas constant = 8.3 J mol−1K−1).
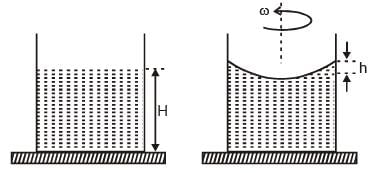
A beaker of radius r is filled with water (refractive index 4/3) up to a height H as shown in the figure on the left. The beaker is kept on a horizontal table rotating with angular speed ω. This makes the water surface curved so that the difference in the height of water level at the center and at the circumference of the beaker is ℎ (h ≪ H, h ≪ r) as shown in the figure on the right. Take this surface to be approximately spherical with a radius of curvature R. Which of the following is/are correct? (g is the acceleration due to gravity)
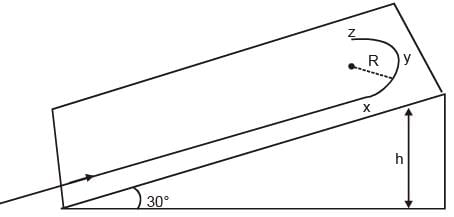
A student skates up a ramp that makes an angle 30° with the horizontal. He/she starts (as shown in the figure) at the bottom of the ramp with speed v0 and wants to turn around over a semicircular path xyz of radius R during which he/she reaches a maximum height h (at point y) from the ground as shown in the figure. Assume that the energy loss is negligible and the force required for this turn at the highest point is provided by his/her weight only. Then (g is the acceleration due to gravity)
A rod of mass m and length L pivoted at one of its ends, is hanging vertically. A bullet of the same mass moving at speed v strikes the rod horizontally at a distance x from its pivoted end and gets embedded in it. The combined system now rotates with angular speed ω about the pivot. The maximum angular speed ωM is achieved for x = xM. Then

In an X-ray tube, electrons emitted from a filament (cathode) carrying current I hit a target (anode) at a distance d from the cathode. The target is kept at a potential V higher than the cathode resulting in emission of continuous and characteristic X-rays. If the filament current I is decreased to I/2, the potential difference V is increased to 2V, and the separation distance d is reduced to d/2, then
Two identical non-conducting solid spheres of same mass and charge are suspended in air from a common point by two non-conducting, massless strings of same length. At equilibrium, the angle between the strings is α. The spheres are now immersed in a dielectric liquid of density 800 kg m−3 and dielectric constant 21. If the angle between the strings remains the same after the immersion, then
Starting at time t = 0 from the origin with speed 1 ms−1, a particle follows a two-dimensional trajectory in the x-y plane so that its coordinates are related by the equation  The x and y components of its acceleration are denoted by ax and ay, respectively. Then,
The x and y components of its acceleration are denoted by ax and ay, respectively. Then,
A spherical bubble inside water has radius R. Take the pressure inside the bubble and the water pressure to be p0. The bubble now gets compressed radially in an adiabatic manner so that its radius becomes (R-a). For a ≪ R the magnitude of the work done in the process is given by (4πp0Ra2)X, where X is a constant and γ = CP/Cv = 41/30. The value of X is _____.
In the balanced condition, the values of the resistances of the four arms of a Wheatstone bridge are shown in the figure below. The resistance R3 has temperature coefficient 0.0004 °C-1. If the temperature of R3 is increased by 100“C the voltage developed between S and T will be _____ volt.

Two capacitors with capacitance values C1 = 2000 ± 10 pF and C2 = 3000 ± 15 pF are connected in series. The voltage applied across this combination is V = 5.00 ± 0.02 V. The percentage error in the calculation of the energy stored in this combination of capacitors is _______.
A cubical solid aluminium (bulk modulus = 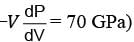 block has an edge length of 1 m on the surface of the earth. It is kept on the floor of a 5 km deep ocean. Taking the average density of water and the acceleration due to gravity to be 103 kg m−3 and 10 ms−2, respectively, the change in the edge length of the block in mm is _____.
block has an edge length of 1 m on the surface of the earth. It is kept on the floor of a 5 km deep ocean. Taking the average density of water and the acceleration due to gravity to be 103 kg m−3 and 10 ms−2, respectively, the change in the edge length of the block in mm is _____.
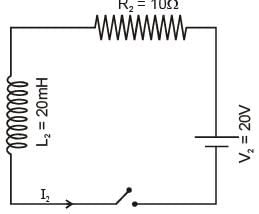
The inductors of two LR circuits are placed next to each other, as shown in the figure. The values of the self-inductance of the indicators, resistance, mutual-inductance and applied voltage are specified in the given circuit. After both the switches are closed simultaneously, the total work done by the batteries against the induced EMF in the inductors by the time the currents reach their steady-state values is________ mJ.

A container with 1 kg of water in it is kept in sunlight, which causes the water to get warmer than the surroundings. The average energy per unit time per unit area received due to the sunlight is 700Wm−2 and it is absorbed by the water over an effective area of 0.05 m2. Assuming that the heat loss from the water to the surroundings is governed by Newton’s law of cooling, the difference (in °C) in the temperature of water and the surroundings after a long time will be _____. (Ignore effect of the container, and take constant for Newton’s law of cooling = 0.001 s−1, Heat capacity of water = 4200 J kg−1 K−1)
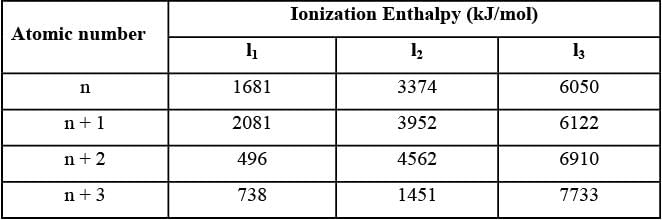
The 1st, 2nd and the 3rd ionization enthalpies I1, I2 and I3, of four atoms with atomic numbers n, n+1, n+2 and n+3 , where n < 10, are tabulated below. What is the value of n?
Consider the following compounds in the liquid form :
O2, HF, H2O, NH3, H2O2, CCl4, CHCl3, C6H6, C6H5Cl.
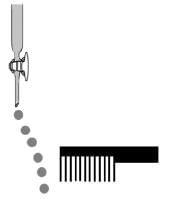
When a charged comb is brought near their flowing stream, how many of them show deflection as per the following figure?
In the chemical reaction between stoichiometric quantities of KMnO4 and KI in weakly basic solution, what is the number of moles of I2 released for 4 moles of KMnO4 consumed?
An acidified solution of potassium chromate was layered with an equal volume of amyl alcohol. When it was shaken after the addition of 1 mL of 3% H2O2, a blue alcohol layer was obtained. The blue color is due to the formation of a chromium (VI) compound 'X'. What is the number of oxygen atoms bonded to chromium through only single bonds in a molecule of X?
The structure of a peptide is given below
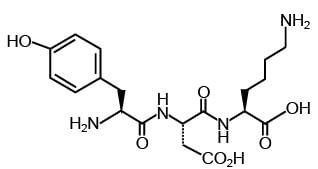
If the absolute values of the net charge of the peptide at pH = 2, pH = 6, and pH = 11 are |z1| , |z2| and |z3|, respectively, then what is |z1| + |z2| + |z3|?
An organic compound (C8H10O2) rotates plane-polarized light. It produce pink color with neutral FeCl3 solution. What is the total number of all the possible isoemrs for this compound?
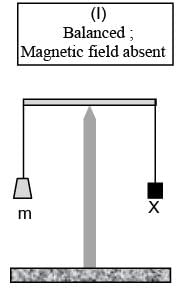
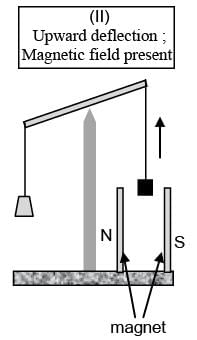
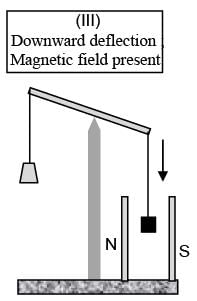
In an experiment, m grams of a compound X (gas/liquid/solid) taken in a container is loaded in a balance as shown in figure I below. In the presence of a magnetic field, the pan with X is either deflected upwards (figure II), or deflected downwards (figure III), depending on the compound X. Identify the correct statement(s)
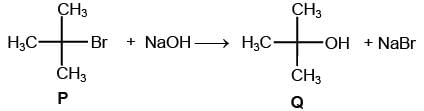
Which of the following plots is(are) correct for the given reaction?
([P]0 is the initial concentration of P)
Which among the following statement(s) is(are) true for the extraction of aluminium from bauxite?
Choose the correct statement(s) among the following.
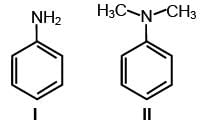
Consider the following four compounds I, II, III, and IV.
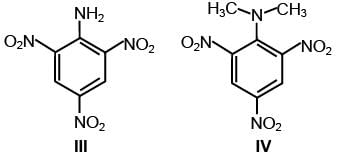
Choose the correct statement(s).
Consider the following transformations of a compound P.
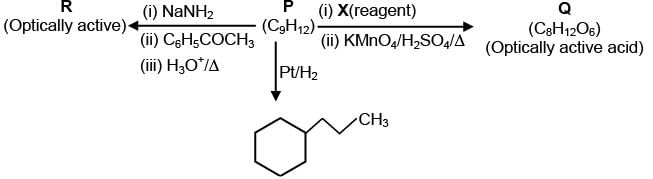
Choose the correct option(s).
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|

















